新人教版数学九年级上册第25章 25.3用频率估计概率 同步训练
试卷更新日期：2016-01-12 类型：同步测试
一、选择题
-
1.
绿豆在相同条件下的发芽试验，结果如下表所示：
每批粒数n
100
300
400
600
1000
2000
3000
发芽的粒数m
96
282
382
570
948
1912
2850
发芽的频数
0.960
0.940
0.955
0.950
0.948
0.956
0.950
则绿豆发芽的概率估计值是（ ）.
A、0.96 B、0.95 C、0.94 D、0.902.某人在做掷硬币实验时，投掷m次，正面朝上有n次（即正面朝上的频率是p= ）．则下列说法中正确的是（ ）。
A、P一定等于
，
B、P一定不等于 ，
C、多投一次，P更接近 ，
D、投掷次数逐渐增加，P稳定在 附近
3. 小明在一只装有红色和白色球各一只的口袋中摸出一只球，然后放回搅匀再摸出一只球，反复多次实验后，发现某种“状况”出现的机会约为50%，则这种状况可能是（ ）.A、两次摸到红色球 B、两次摸到白色球 C、两次摸到不同颜色的球 D、先摸到红色球，后摸到白色球4. 一个密闭不透明的盒子里有若干个白球，在不允许将球倒出来的情况下，为估计白球的个数，小刚向其中放入8个黑球，摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中88次摸到黑球，估计盒中大约有白球（ ）.A、28个 B、30个 C、36个 D、42个5.为验证“掷一个质地均匀的骰子，向上的点数为偶数的概率是0.5”，下列模拟实验中，不科学的是（ ）.
A、袋中装有1个红球一个绿球，它们除颜色外都相同，计算随机摸出红球的概率 B、用计算器随机地取不大于10的正整数，计算取得奇数的概率 C、随机掷一枚质地均匀的硬币，计算正面朝上的概率 D、如图，将一个可以自由旋转的转盘分成甲、乙、丙3个相同的扇形，转动转盘任其自由停止，计算指针指向甲的概率6. 从口袋中随机摸出一球，再放回口袋中，不断重复上述过程，共摸了150次，其中有50次摸到黑球，已知口袋中有黑球10个和若干个白球，由此估计口袋中大约有多少个白球（ ）.A、10个 B、20个 C、30个 D、无法确定7. 小鸡孵化场孵化出1000只小鸡，在60只上做记号，再放入鸡群中让其充分跑散，再任意抓出50只，其中做有记号的大约是( )A、40只 B、25只 C、15只 D、3只8. 一个不透明的盒子里有n个除颜色外其它完全相同的小球，其中有6个黄球．每次摸球前先将盒子里的球摇匀，任意摸出一个球记下颜色后在放回盒子，通过大量重复摸球实验后发现，摸到黄球的频率稳定在30%，那么可以推算出n大约是（ ）.A、6 B、10 C、18 D、209. 一个盒子里装有若干个红球和白球，每个球除颜色以外都相同.5位同学进行摸球游戏，每位同学摸10次(摸出1球后放回，摇匀后再继续摸)，其中摸到红球数依次为8，5，9，7，6，则估计盒中红球和白球的个数是( )A、红球比白球多 B、白球比红球多 C、红球，白球一样多 D、无法估计10. 关于频率和概率的关系，下列说法正确的是（ ）.A、频率等于概率； B、当实验次数很大时，频率稳定在概率附近； C、当实验次数很大时，概率稳定在频率附近； D、实验得到的频率与概率不可能相等11.在学习掷硬币的概率时，老师说：“掷一枚质地均匀的硬币，正面朝上的概率是
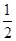”，小明做了下列三个模拟实验来验证．①取一枚新硬币，在桌面上进行抛掷，计算正面朝上的次数与总次数的比值；
②把一个质地均匀的圆形转盘平均分成偶数份，并依次标上奇数和偶数，转动转盘，计算指针落在奇数区域的次数与总次数的比值；
③将一个圆形纸板放在水平的桌面上，纸板正中间放一个圆锥（如图），从圆锥的正上方往下撒米粒，计算其中一半纸板上的米粒数与纸板上总米粒数的比值． 上面的实验中，不科学的有（ ）.
A、0个 B、1个 C、2个 D、3个12. 抛掷两枚均匀的硬币，当抛掷多次以后，出现两个反面的成功率大约稳定在（ ）.A、25% B、50% C、75% D、100%13. 下列说法正确的是（ ）.①试验条件不会影响某事件出现的频率；
②在相同的条件下试验次数越多，就越有可能得到较精确的估计值，但各人所得的值不一定相同；
③如果一枚骰子的质量分布均匀，那么抛掷后每个点数出现的机会均等；
④抛掷两枚质量分布均匀的相同的硬币，出现“两个正面”、“两个反面”、“一正一反”的机会相同．
A、①② B、②③ C、③④ D、①③14. 小明练习射击，共射击60次，其中有38次击中靶子，由此可估计，小明射击一次击中靶子的概率是（ ）.A、38% B、60% C、约63% D、无法确定15. 在一个不透明的盒子中，红色、白色、黑色的球共有40个，除颜色外其他完全相同，老师在课堂上组织同学通过多次试验后发现其中摸到红色、白色的频率基本稳定在45%和15%，则盒子中黑色球的个数可能是（ ）.A、16 B、18 C、20 D、22二、填空题
-
16. 有一箱规格相同的红、黄两种颜色的小塑料球共1000个．为了估计这两种颜色的球各有多少个，小明将箱子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回箱子中，多次重复上述过程后．发现摸到红球的频率约为0.6，据此可以估计红球的个数约为 ．17. 在“抛掷正六面体”的试验中，如果正六面体的六个面分别标有数字“1”、“2”、“3”、“4”、“5”和“6”，如果试验的次数增多，出现数字“1”的频率的变化趋势是.18. 从某玉米种子中抽取6批，在同一条件下进行发芽试验，有关数据如下：
种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
85
298
652
793
1604
4005
发芽频率
0.850
0.745
0.815
0.793
0.802
0.801
根据以上数据可以估计，该玉米种子发芽的概率约为（精确到0.1）．
19. 晓刚用瓶盖设计了一个游戏：任意掷出一个瓶盖，如果盖面朝上则甲胜，如果盖面朝下则乙胜，你认为这个游戏（是否公平）；如果以硬币代替瓶盖，同样做上述游戏，你认为这个游戏（是否公平）．20. 一个不透明的袋中装有2枚白色棋子和n枚黑色棋子，它们除颜色不同外，其余均相同．若小明从中随机摸出一枚棋子，多次实验后发现摸到黑色棋子的频率稳定在80%．则n很可能是枚．三、解答题
-
21. 某商场为了吸引顾客，举行抽奖活动，并规定：顾客每购买100元的商品，就可随机抽取一张奖券，抽得奖券“紫气东来”、“花开富贵”、“吉星高照”，就可以分别获得100元、50元、20元的购物券，抽得“谢谢惠顾”不赠购物券；如果顾客不愿意抽奖，可以直接获得购物券10元．小明购买了100元的商品，他看到商场公布的前10000张奖券的抽奖结果如下：
奖券种类
紫气东来
花开富贵
吉星高照
谢谢惠顾
出现张数（张）
500
1000
2000
6500
(1)、求“紫气东来”奖券出现的频率；(2)、请你帮助小明判断，抽奖和直接获得购物券，哪种方式更合算？并说明理由．22. 研究问题：一个不透明的盒中装有若干个只有颜色不一样的红球与黄球，怎样估算不同颜色球的数量？
操作方法：先从盒中摸出8个球，画上记号放回盒中，再进行摸球实验，摸球实验的要求：先搅拌均匀，每次摸出一个球，放回盒中，再继续．
活动结果：摸球实验活动一共做了50次，统计结果如下表：球的颜色
无记号
有记号
红色
黄色
红色
黄色
摸到的次数
18
28
2
2
推测计算：由上述的摸球实验可推算：
(1)、盒中红球、黄球各占总球数的百分比分别是多少？
(2)、盒中有红球多少个？
23. 端午节吃粽子是中华民族的传统习俗，五月初五早上，奶奶为小明准备了四只粽子：一只肉馅，一只香肠馅，两只红枣馅，四只粽子除内部馅料不同外其他均一切相同．小明喜欢吃红枣馅的粽子．(1)、请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率；(2)、在吃粽子之前，小明准备用一个均匀的正四面体骰子（如图所示）进行吃粽子的模拟试验，规定：掷得点数1向上代表肉馅，点数2向上代表香肠馅，点数3，4向上代表红枣馅，连续抛掷这个骰子两次表示随机吃两只粽子，从而估计吃两只粽子刚好都是红枣馅的概率．你认为这样模拟正确吗？试说明理由．
24.如图，均匀的正四面体的各面依次标有1，2，3，4四个数字．小明做了60次投掷试验，结果统计如下
：朝下数字
1
2
3
4
出现的次数
16
20
14
10
(1)、计算上述试验中“4朝下”的频率是多少？(2)、“根据试验结果，投掷一次正四面体，出现2朝下的概率是
．”的说法正确吗？为什么？(3)、随机投掷正四面体两次，请用列表或画树状图法，求两次朝下的数字之和大于4的概率．
25. 一粒木质中国象棋子“兵”，它的正面雕刻一个“兵”字，它的反面是年平的．将它从一定高度下掷，落地反弹后可能是“兵”字面朝上，也可能是“兵”字面朝下．由于棋子的两面不均匀，为了估计“兵”字面朝上的概率，某实验小组做了棋子下掷实验，实验数据如下表：实验次数
20
40
60
80
100
120
140
160
“兵”字面朝上频数
14
38
47
52
66
78
88
相应频率
0.7
0.45
0.63
0.59
0.52
0.56
0.55
(1)、请将数据补充完整；实验次数
20
40
60
80
100
120
140
160
“兵”字面朝上频数
14
38
47
52
66
78
88
相应频率
0.7
0.45
0.63
0.59
0.52
0.56
0.55
(2)、画出“兵”字面朝上的频率分布折线图；
(3)、如果实验继续进行下去，根据上表的数据，这个实验的频率将稳定在它的概率附近，请你估计这个概率是多少？