2016-2017学年山东省滨州市七年级下学期期中数学试卷
试卷更新日期:2017-06-27 类型:期中考试
一、选择题
-
1. 数5的算术平方根为( )A、 B、25 C、±25 D、±2. 下面四个图形中,∠1与∠2是邻补角的是( )A、
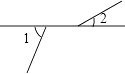 B、
B、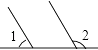 C、
C、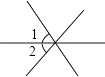 D、
D、 3. 下列说法正确地有( )
3. 下列说法正确地有( )1)点(1,﹣a)一定在第四象限 (2)坐标轴上的点不属于任一象限 (3)若点(a,b)在坐标轴的角平分线上,则a=b (4)直角坐标系中,在y轴上且到原点的距离为5的点的坐标是(0,5)
A、1个 B、2个 C、3个 D、4个4. 如图,CF是△ABC的外角∠ACM的平分线,且CF∥AB,∠ACF=50°,则∠B的度数为( )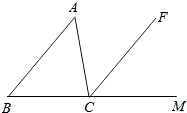 A、80° B、40° C、60° D、50°5. 如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )
A、80° B、40° C、60° D、50°5. 如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )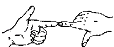 A、同位角 B、内错角 C、对顶角 D、同旁内角6. 若 是关于x.y的方程2x﹣y+2a=0的一个解,则常数a为( )A、1 B、2 C、3 D、47. 如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
A、同位角 B、内错角 C、对顶角 D、同旁内角6. 若 是关于x.y的方程2x﹣y+2a=0的一个解,则常数a为( )A、1 B、2 C、3 D、47. 如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )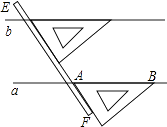 A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,内错角相等8. 下列各式正确的是( )A、 =3 B、(﹣ )2=16 C、 =±3 D、 =﹣49. 在实数:3.14159, ,1.010010001,4.21,π, 中,无理数有( )A、1个 B、2个 C、3个 D、4个10. 如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,内错角相等8. 下列各式正确的是( )A、 =3 B、(﹣ )2=16 C、 =±3 D、 =﹣49. 在实数:3.14159, ,1.010010001,4.21,π, 中,无理数有( )A、1个 B、2个 C、3个 D、4个10. 如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )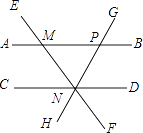 A、∠EMB=∠END B、∠BMN=∠MNC C、∠CNH=∠BPG D、∠DNG=∠AME11. 如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
A、∠EMB=∠END B、∠BMN=∠MNC C、∠CNH=∠BPG D、∠DNG=∠AME11. 如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( ) A、50° B、30° C、20° D、15°12. 李明同学早上骑自行车上学,中途因道路施工步行一段路,到学校共用时15分钟.他骑自行车的平均速度是250米/分钟,步行的平均速度是80米/分钟.他家离学校的距离是2900米.如果他骑车和步行的时间分别为x、y分钟,列出的方程是( )A、 B、 C、 D、
A、50° B、30° C、20° D、15°12. 李明同学早上骑自行车上学,中途因道路施工步行一段路,到学校共用时15分钟.他骑自行车的平均速度是250米/分钟,步行的平均速度是80米/分钟.他家离学校的距离是2900米.如果他骑车和步行的时间分别为x、y分钟,列出的方程是( )A、 B、 C、 D、二、填空题
-
13. 已知点M(a,b),且a•b>0,a+b<0,则点M在第象限.14. 如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为cm2 .
 15. 点A(m+3,m+1)在x轴上,则点A坐标为 .16. 如图所示的象棋盘上,若帅位于点(1,﹣2)上,相位于点(3,﹣2)上,则炮所在点的坐标是 .
15. 点A(m+3,m+1)在x轴上,则点A坐标为 .16. 如图所示的象棋盘上,若帅位于点(1,﹣2)上,相位于点(3,﹣2)上,则炮所在点的坐标是 .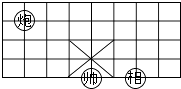 17. 如图,有一条直的宽纸带,按图折叠,则∠α的度数等于 .
17. 如图,有一条直的宽纸带,按图折叠,则∠α的度数等于 .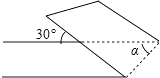 18. = .19. 已知5+ 的小数部分为a,5﹣ 的小数部分为b,则(a+b)2017= .
18. = .19. 已知5+ 的小数部分为a,5﹣ 的小数部分为b,则(a+b)2017= .三、解答题
-
20. 根据要求,解答下列问题(1)、解下列方程组(直接写出方程组的解即可)
① 的解为② 的解为③ 的解为
(2)、以上每个方程组的解中,x值与y值的大小关系为 .(3)、请你构造一个具有以上外形特征的方程组,并直接写出它的解.21.如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1 , 点P的对应点为P1(a+6,b﹣2 ).
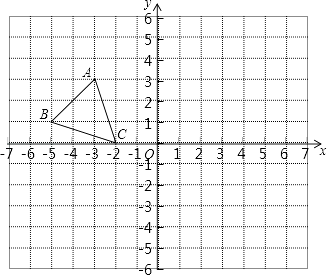 (1)、直接写出点A1 , B1 , C1的坐标.(2)、在图中画出△A1B1C1 .(3)、连接A A1 , 求△AOA1的面积.22. 如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,试判断DG与BC的位置关系,并说明理由.
(1)、直接写出点A1 , B1 , C1的坐标.(2)、在图中画出△A1B1C1 .(3)、连接A A1 , 求△AOA1的面积.22. 如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,试判断DG与BC的位置关系,并说明理由.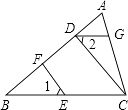 23. 如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.
23. 如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AB∥CD.
 24. 已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=50°,求:∠BHF的度数.
24. 已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=50°,求:∠BHF的度数.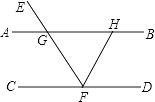 25. 某服装点用6000购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
25. 某服装点用6000购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.类型
价格
A型
B型
进价(元/件)
60
100
标价(元/件)
100
160
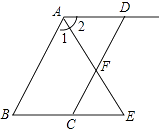
(1)、求这两种服装各购进的件数;(2)、如果A种服装按标价的8折出售,B种服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?26. 小明用《几何画板》画图,他先画了两条平行线AB、CD,然后在平行线间画了一点E,连接BE,DE后(如图①),它用鼠标左键点住点E,拖动后,分别得到如图②、③、④等图形,这时他突然一想,∠B、∠D与∠BED之间的度数有没有某种联系呢?接着小明同学通过利用《几何画板》的“度量角度”和“计算”的功能,找到了这三个角之间的关系.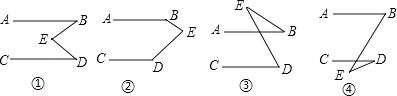 (1)、请你分别写出图①至图④各图中的∠B、∠D与∠BED之间关系;(2)、证明从图③中得到的结论.
(1)、请你分别写出图①至图④各图中的∠B、∠D与∠BED之间关系;(2)、证明从图③中得到的结论.