初中数学北师大版九年级上学期 第一章测试卷

试卷更新日期：2019-09-19 类型：单元试卷

进入 出卷网 下载

一、单选题

  • 1. 矩形不一定具有的性质是（   ）
    A、对角线互相平分 B、对角线互相垂直     C、对角线相等 D、是轴对称图形

    查看试题解析

  • 2. 下列说法正确的是（ ）
    A、一组对边平行，另一组对边相等的四边形是平行四边形 B、对角线相等的平行四边形是菱形 C、三个角都是直角的四边形是矩形 D、一组邻边相等的平行四边形是正方形

    查看试题解析

  • 3. 下列说法错误的是（   ）
    A、连接对角线互相垂直的四边形各边中点所得的四边形是矩形 B、连接对角线互相平分的四边形各边中点所得的四边形是平行四边形 C、连接对角线相等的梯形各边中点所得的四边形是菱形 D、连接对角线互相垂直平分的四边形各边中点所得的四边形是正方形

    查看试题解析

  • 4. 在平面直角坐标系中，矩形 ABCD 的顶点 A ， B ， C 的坐标分别为 (−2 ， 0) ， (2 ， 0) ， (2 ， 3) ，则顶点 D 的坐标是 (    )
    A、(−2 ， 3) B、(−2 ， −3) C、(2 ， 3) D、(2 ， −3)

    查看试题解析

  • 5. 在正方形ABCD中，E、F是对角线AC上两点连接BE、BF、DE、DF，则A添加下列哪一个条件可以判定四边形BEDF是菱形（   ）

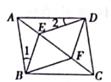    A、∠1=∠2 B、BE=DF C、∠EDF=60° D、AB=AF

    查看试题解析

  • 6. 如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，AB＝6cm，BC＝8cm，则△AEF的周长是（   ）

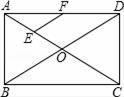    A、14cm B、8cm C、9cm D、10cm

    查看试题解析

  • 7. 如图，正方形ABCD的边长为3，点EF在正方形ABCD内若四边形AECF恰是菱形连结FB，DE，且AF2-FB2=3，则菱形AECF的边长为（ ）．

    A、2 B、3 C、2 D、5

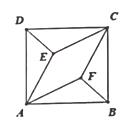    查看试题解析

  • 8. 在△ABC中，AB=3，AC=4，BC=5，点P为边BC上一动点，PE⊥AB于点E，PF⊥AC于点F，则EF的最小值为（   ）
    A、2.5 B、2.4 C、2.2 D、2

    查看试题解析

二、填空题

  • 9. 如图，矩形ABCD中，AD=5，AB=7.点E为DC上一个动点，把△ADE沿AE折叠，当点D的对应点D'落在∠ABC的角平分线上时，DE的长为.

    查看试题解析

  • 10. 如图，在正方形ABCD中，G是对角线BD上的点，GE⊥CD，GF⊥BC，E、F分别为垂足，连结EF，设M，N分别是AB，BG的中点，EF=5，则MN的长为。

    查看试题解析

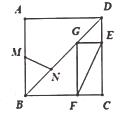
三、作图题

  • 11. 图1，图2，图3是三张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，A，C两点都在格点上，连结AC，请完成下列作图：

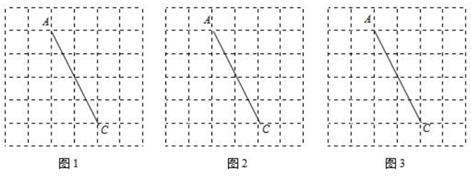    (1)、以AC为对角线在图1中作一个正方形，且正方形各顶点均在格点上
    (2)、以AC为对角线在图2中作一个矩形，使得矩形面积为6，且矩形各顶点均在格点上
    (3)、以AC为对角线在图3中作一个面积最小的平行四边形，且平行四边形各顶点均在格点上

    查看试题解析

四、综合题

  • 12. 如图，在△ABC中，D、F分别是BC、AC边的中点，连接DA、DF，且AD=2DF，过点B作AD的平行线交FD的延长线于点E．

    (1)、求证：四边形ABED为菱形；
    (2)、若BD=6，∠E=60°，求四边形ABEF的面积．

    查看试题解析

  • 13. 如图，将一张矩形纸片 ABCD 沿直线 MN 折叠，使点 C 落在点 A 处，点 D 落在点 E 处，直线 MN 交 BC 于点 M ，交 AD 于点 N .

    (1)、求证： CM=CN ；
    (2)、若 ΔCMN 的面积与 ΔCDN 的面积比为 3：1 ， ND=1 .

    ①求 MC 的长.

    ②求 MN 的长.

    查看试题解析

  • 14. 如图1，在正方形ABCD中，点E ， F分别是AC ， BC上的点，且满足DE ⊥EF ， 垂足为点E ， 连接DF.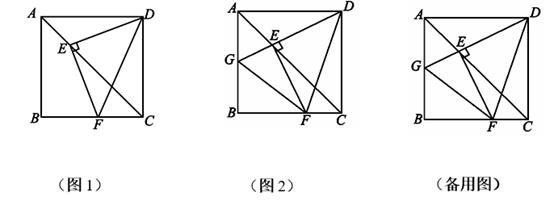

    (1)、求∠EDF=(填度数)；
    (2)、延长DE交AB于点G ， 连接FG ， 如图2，猜想AG ， GF ， FC三者的数量关系，并给出证明；
    (3)、①若AB=6，G 是AB 的中点，求△BFG的面积；

    ②设AG = a ，CF = b ，△BFG 的面积记为S ， 试确定S与 a ， b 的关系，并说明理由.

    查看试题解析