初中数学北师大版九年级上学期 第一章 1.3 正方形的性质与判定
试卷更新日期:2019-09-19 类型:同步测试
一、单选题
-
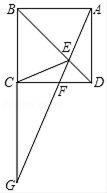
1. 下列命题是真命题的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是矩形 C、对角线互相垂直的矩形是正方形 D、四边相等的平行四边形是正方形2. 如图,边长为的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM=( )
 A、 B、 C、 D、3. 把边长分别为1和2的两个正方形按如图的方式放置.则图中阴影部分的面积为( )
A、 B、 C、 D、3. 把边长分别为1和2的两个正方形按如图的方式放置.则图中阴影部分的面积为( )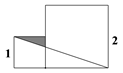 A、 B、 C、 D、4. 如图,正方形 ,点 在边 上,且 , ,垂足为 ,且交 于点 , 与 交于点 ,延长 至 ,使 ,连接 .有如下结论:① ;② ;③ ;④ .上述结论中,所有正确结论的序号是( )
A、 B、 C、 D、4. 如图,正方形 ,点 在边 上,且 , ,垂足为 ,且交 于点 , 与 交于点 ,延长 至 ,使 ,连接 .有如下结论:① ;② ;③ ;④ .上述结论中,所有正确结论的序号是( )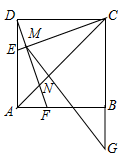 A、①② B、①③ C、①②③ D、②③④5. 如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )
A、①② B、①③ C、①②③ D、②③④5. 如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )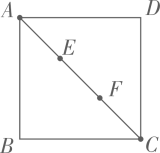 A、0 B、4 C、6 D、86. 已知正方形的对称中心在坐标原点,顶点 按逆时针依次排列,若点 的坐标为 ,则 点与 点的坐标分别为( )A、 B、 C、 D、7. 如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为( )
A、0 B、4 C、6 D、86. 已知正方形的对称中心在坐标原点,顶点 按逆时针依次排列,若点 的坐标为 ,则 点与 点的坐标分别为( )A、 B、 C、 D、7. 如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为( )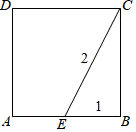 A、 B、3 C、 D、58. 在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+S2+S3+S4等于( )
A、 B、3 C、 D、58. 在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+S2+S3+S4等于( ) A、4 B、5 C、6 D、149. 将正方形纸片按如图折叠,若正方形纸片边长为4,则图片中MN的长为
A、4 B、5 C、6 D、149. 将正方形纸片按如图折叠,若正方形纸片边长为4,则图片中MN的长为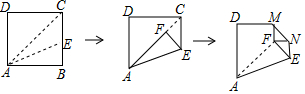 A、1 B、2 C、
A、1 B、2 C、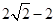 D、
D、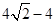
二、填空题
-
10. 平行四边形ABCD的对角线AC与BD相交于点D,且AC⊥BD,请添加一个条件: , 使得平行四边形ABCD为正方形.
11. 如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为. 12. 如图,在正方形ABCD中,BE=1,将BC沿CE翻折,使B点对应点刚好落在对角线AC上,将AD沿AF翻折,使D点对应点刚好落在对角线AC上,求EF= .
12. 如图,在正方形ABCD中,BE=1,将BC沿CE翻折,使B点对应点刚好落在对角线AC上,将AD沿AF翻折,使D点对应点刚好落在对角线AC上,求EF= . 13. 图中两个正方形的中心重合,小正方形的顶点A、C两点在大正方形的对角形上,△HAC是等边三角形,若AB=2,则大正方形的边长为 .
13. 图中两个正方形的中心重合,小正方形的顶点A、C两点在大正方形的对角形上,△HAC是等边三角形,若AB=2,则大正方形的边长为 .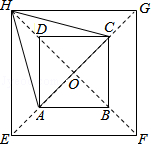
三、解答题
-
14. 如图,ABCD是正方形,E是CD边上任意一点,连接AE,作BF⊥AE,DG垂直AE,垂足分别为F,G.求证:BF-DG=FG.
 15. 如图,正方形ABCD的对角线AC、BD相交于点O,E是OC上一点,连接EB.过点A作 ,垂足为M,AM与BD相交于点F.求证: .
15. 如图,正方形ABCD的对角线AC、BD相交于点O,E是OC上一点,连接EB.过点A作 ,垂足为M,AM与BD相交于点F.求证: .
四、综合题