初中数学北师大版九年级上学期 第一章 1.2 矩形的性质与判定
试卷更新日期：2019-09-19 类型：同步测试
一、单选题
-
1. 下列结论中，矩形具有而菱形不一定具有的性质是（ ）A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直2. 四边形ABCD的对角线互相平分，要使它变为矩形，需要添加的条件是（ ）A、AB=CD B、AB=BC C、AC⊥BD D、AC=BD3. 对于任意的矩形，下列说法一定正确的是（ ）A、对角线垂直且相等 B、四边都互相垂直 C、四个角都相等 D、是轴对称图形，但不是中心对称图形4. 如图，矩形ABCD的对角线交于点O．若∠BAO=55°，则∠AOD等于（ ）
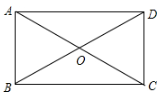A、110° B、115° C、120° D、125°5. 如图，矩形内有两个相邻的正方形，其面积分别为2和8，则图中阴影部分的面积为（ ）
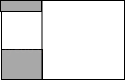A、 B、2 C、 D、66. 正方形ABCD的边AB上有一动点E，以EC为边作矩形ECFG，且边FG过点D，在点E从点A移动到点B的过程中，矩形ECFG的面积（ ）
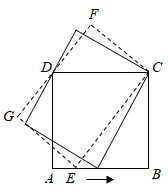A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变7. 将矩形ABCD按如图所示的方式折叠，BE，EG，FG为折痕，若顶点A，C，D都落在点O处，且点B，O，G在同一条直线上，同时点E，O，F在另一条直线上，则 的值为（ ）
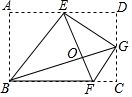A、 B、 C、 D、8. 如图，在矩形ABCD中，AB=3，BC=6，若点E，F分别在AB，CD上，且BE=2AE，DF=2FC，G，H分别是AC的三等分点，则四边形EHFG的面积为（ ）
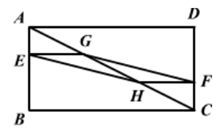A、1 B、 C、2 D、49. 将三角尺按如图所示放置在一张矩形纸片上， ， ， ，则 的度数为（ ）
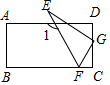A、130° B、120° C、110° D、100°10. 如图，将一长方形纸片沿着虚线剪成两个全等的梯形纸片.根据图中标示长度与角度，求梯形纸片中较短的底边长度为何？（ ）
A、4 B、5 C、6 D、7二、填空题
-
11. 如图，在Rt△ABC中，∠BAC＝900 ， 且BA＝3，AC＝4，点D是斜边BC上的一个动点，过点D分别作DM⊥AB于点M，DN⊥AC于点N，连接MN，则线段MN的最小值为.
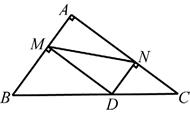12. 在矩形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的点（不与端点重合）．对于任意矩形ABCD，下面四个结论中，①存在无数个四边形MNPQ是平行四边形；②存在无数个四边形MNPQ是矩形；③存在无数个四边形MNPQ是菱形；④至少存在一个四边形MNPQ是正方形．所有正确结论的序号是 ．三、综合题
-
13. 如图，矩形ABCD中，AB＝8，AD＝6，点O是对角线BD的中点，过点O的直线分别交AB、CD边于点E、F.
(1)、求证：四边形DEBF是平行四边形；(2)、当DE＝DF时，求EF的长.14. 已知：在矩形ABCD中，BD是对角线，AE⊥BD于点E，CF⊥BD于点F．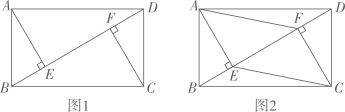
(1)、如图1，求证：AE=CF；(2)、如图2，当∠ADB=30°时，连接AF、CE，在不添加任何辅助线的情况下，请直接写出图2中四个三角形，使写出的每个三角形的面积都等于矩形ABCD面积的 ．15. 如图，在平面直角坐标系中，O是原点，点A在x轴的负半轴上，点B在y轴的正半轴上，AO=2OB，且线段OB的长是方程x2-2x-8=0的一个根．
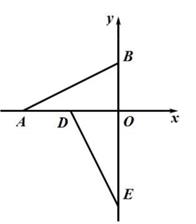(1)、求直线AB的函数解析式．(2)、将△ABD绕点O逆时针方向旋转90°得到△EDO，直线ED交线段AB 于点C，点F是直线CE上一点，分别过点E、F作x轴和y轴的平行线交于点G，将△EFG沿EF折叠，使点G的对应点落在坐标轴上，求点F的坐标．(3)、在(2)的条件下，点M是DO中点，点N、P、Q在直线BD或者y轴上，是否存在点P，使四边形MNPQ是矩形?若存在，请利用备用图画出示意图并直接写出点P的坐标；若不存在，请说明理由．