初中数学浙教版九年级上册3.8 弧长及扇形的面积——弧长 同步训练
试卷更新日期:2019-09-19 类型:同步测试
一、单选题
-
1. 如图,小正方形的边长均为1,扇形OAB是某圆锥的侧面展开图,则这个圆锥的底面周长为( )
 A、 B、 C、2 D、32. 如果一个扇形的半径是3,弧长是π,那么此扇形的圆心角的大小为( )A、30° B、45° C、60° D、90°3. 如图,⊙O的直径AB=6,若∠BAC=50°,则劣弧AC的长为( )
A、 B、 C、2 D、32. 如果一个扇形的半径是3,弧长是π,那么此扇形的圆心角的大小为( )A、30° B、45° C、60° D、90°3. 如图,⊙O的直径AB=6,若∠BAC=50°,则劣弧AC的长为( ) A、2π B、
A、2π B、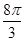 C、
D、
C、
D、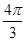 4. 如图,在 中, , , ,扇形AOC的圆心角为 ,点D为 上一动点,P为BD的中点,当点D从点A运动至点C,则点P的运动路径长为( )
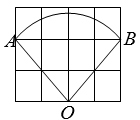
4. 如图,在 中, , , ,扇形AOC的圆心角为 ,点D为 上一动点,P为BD的中点,当点D从点A运动至点C,则点P的运动路径长为( )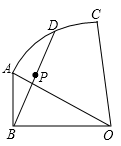 A、1 B、 C、 D、5. 如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则弧HR的弧长为( )
A、1 B、 C、 D、5. 如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则弧HR的弧长为( )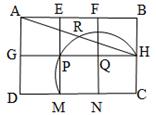 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
6. 如图,圆锥的底面半径为1 cm,母线AB的长为3 cm,则这个圆锥侧面展开图扇形的圆心角为度.
 7. 如图,在□ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则 的长为 .
7. 如图,在□ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则 的长为 .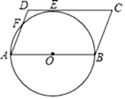 8. 如图△ABC中,∠A=30°,∠C=90°,作△ABC的外接圆.若弧AB的长为12cm,那么弧AC的长是.
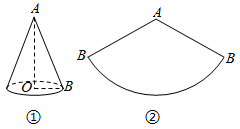
8. 如图△ABC中,∠A=30°,∠C=90°,作△ABC的外接圆.若弧AB的长为12cm,那么弧AC的长是. 9. 通过对课本中《硬币滚动中的数学》的学习,我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程(如图①).在图②中,有2014个半径为r的圆紧密排列成一条直线,半径为r的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位,则动圆C自身转动的周数为 .
9. 通过对课本中《硬币滚动中的数学》的学习,我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程(如图①).在图②中,有2014个半径为r的圆紧密排列成一条直线,半径为r的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位,则动圆C自身转动的周数为 .
三、解答题
-
10. 如图,在△ABC中,∠ACB=90°,∠B=25°,CA=3,以点C为圆心,CA长为半径的圆交AB于点D,求弧AD的长。
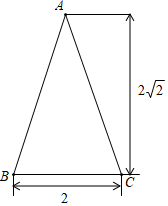
 11. 如图,把Rt△ABC的斜边放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″位置.设BC=1,AC= ,求当顶点A运动到A″位置时,点A经过的路线长度.
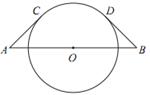
11. 如图,把Rt△ABC的斜边放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″位置.设BC=1,AC= ,求当顶点A运动到A″位置时,点A经过的路线长度.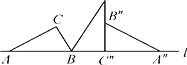 12. 如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
12. 如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC. (1)、求证:AE=ED;(2)、若AB=10,∠CBD=36°,求 的长.
(1)、求证:AE=ED;(2)、若AB=10,∠CBD=36°,求 的长.四、中考演练
-
13. 如图,线段 AB 经过⊙O 的圆心, AC , BD 分别与⊙O 相切于点 C ,D .若 AC =BD = 4 ,∠A=45°,则弧CD的长度为( )
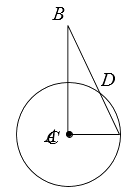
 A、π B、2π C、2 π D、4π14. 如图,将 沿弦 折叠, 恰好经过圆心 ,若 的半径为3,则 的长为( )
A、π B、2π C、2 π D、4π14. 如图,将 沿弦 折叠, 恰好经过圆心 ,若 的半径为3,则 的长为( )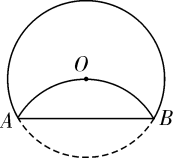 A、 B、 C、 D、
A、 B、 C、 D、