初中数学浙教版九年级上册3.7 正多边形 强化提升训练
试卷更新日期:2019-09-19 类型:同步测试
一、综合提升
-
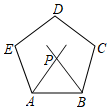
1. 如图,五边形ABCDE是正五边形,若l1∥l2 , 则∠1-∠2的值为( )。
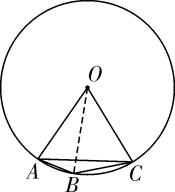
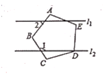 A、180° B、108° C、90° D、72°2. 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
A、180° B、108° C、90° D、72°2. 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )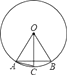 A、弦AB的长等于圆内接正六边形的边长 B、弦AC的长等于圆内接正十二边形的边长 C、 D、∠BAC=30°3. 如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
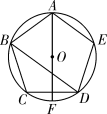
A、弦AB的长等于圆内接正六边形的边长 B、弦AC的长等于圆内接正十二边形的边长 C、 D、∠BAC=30°3. 如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )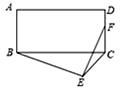 A、 B、4 C、5 D、4. 如图,正五边形ABCDE内接于⊙O点F为 的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )
A、 B、4 C、5 D、4. 如图,正五边形ABCDE内接于⊙O点F为 的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( ) A、36° B、54° C、60° D、72°5. 一个正方形、一个等边三角形和一个正五边形如图摆放,若∠3=36°,则∠1+∠2的大小是度.
A、36° B、54° C、60° D、72°5. 一个正方形、一个等边三角形和一个正五边形如图摆放,若∠3=36°,则∠1+∠2的大小是度.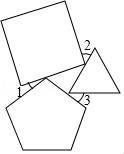 6. 在图中,含30°的直角三角板的直角边AC,BC分别经过正八边形的两个顶点,则图中∠1+∠2= .
6. 在图中,含30°的直角三角板的直角边AC,BC分别经过正八边形的两个顶点,则图中∠1+∠2= .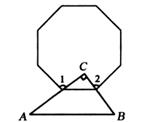 7. 如图,AB,AC分别为⊙O的内接正六边形,内接正方形的一边,BC是圆内接n边形的一边,则n等于.
7. 如图,AB,AC分别为⊙O的内接正六边形,内接正方形的一边,BC是圆内接n边形的一边,则n等于.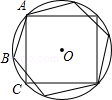 8. 如图,作半径为2的⊙O的内接正四边形ABCD,然后作正四边形ABCD的内切圆,得第二个圆,再作第二个圆的内接正四边形A1B1C1D1 , 又作正四边形A1B1C1D1的内切圆,得第三个圆…,如此下去,则第六个圆的半径为 .
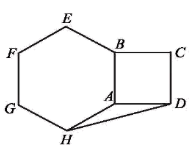
8. 如图,作半径为2的⊙O的内接正四边形ABCD,然后作正四边形ABCD的内切圆,得第二个圆,再作第二个圆的内接正四边形A1B1C1D1 , 又作正四边形A1B1C1D1的内切圆,得第三个圆…,如此下去,则第六个圆的半径为 .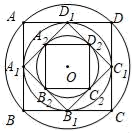 9. 如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
9. 如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):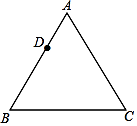 (1)、作△ABC的外心O;(2)、设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.10. 如图,有一个圆O和两个正六边形T1 , T2 . T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1 , T2分别为圆O的内接正六边形和外切正六边形).
(1)、作△ABC的外心O;(2)、设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.10. 如图,有一个圆O和两个正六边形T1 , T2 . T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1 , T2分别为圆O的内接正六边形和外切正六边形).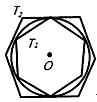 (1)、设T1 , T2的边长分别为a,b,圆O的半径为r,求r:a及r:b的值;(2)、求正六边形T1 , T2的面积比S1:S2的值.
(1)、设T1 , T2的边长分别为a,b,圆O的半径为r,求r:a及r:b的值;(2)、求正六边形T1 , T2的面积比S1:S2的值.二、中考演练
-
11. 如图,以正方形ABCD的AB边向外作正六边形ABEFGH,连接DH,则∠ADH=°
 12. 如图,该硬币边缘镌刻的正九边形每个内角的度数是 .
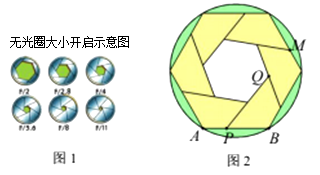
12. 如图,该硬币边缘镌刻的正九边形每个内角的度数是 . 13. 用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形 .图中, 度.
13. 用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形 .图中, 度.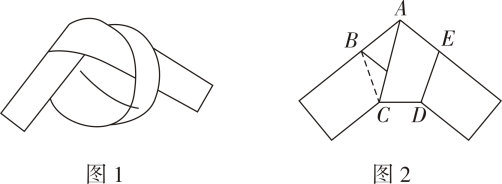 14. 如图所示,过正五边形 的顶点 作一条射线与其内角 的角平分线相交于点 ,且 ,则 度.
14. 如图所示,过正五边形 的顶点 作一条射线与其内角 的角平分线相交于点 ,且 ,则 度.