初中数学浙教版九年级上册3.6 圆内接四边形 强化提升训练
试卷更新日期：2019-09-19 类型：同步测试
一、综合提升
-
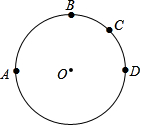
1. 如图，四边形ABCD内接于⊙O，F是 上一点，且 = ，连接CF并延长交AD的延长线于点E，连接AC，若∠ABC=105°，∠BAC=25°，则∠E的度数为（ ）
A、45° B、50° C、55° D、60°2. 如图，A，B是⊙O上的两点，C是⊙O上不与A，B重合的任意一点.如果∠AOB＝130°，那么∠ACB的度数为（ ）
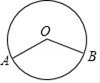A、65° B、115° C、130° D、65°或115°3. 如图，在⊙O中，直径AB垂直弦CD，E为BC弧上一点，下列结论：①∠1=∠2；②∠3=2∠4；③∠3+∠5=180°，其中正确的是（ ）
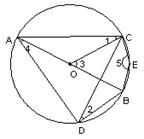A、①③ B、②③ C、①②③ D、①②4. 如图，AB为⊙O的直径，C为 上一点，AD∥OC， AD交⊙O于点D，连接AC，CD，设∠BOC=x°，∠ACD=y°，则下列结论成立的是（ ）
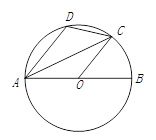A、x+y=90 B、2x+y=90 C、2x+y=180 D、x=y5. 已知AB是半径为1的圆O的一条弦，且AB=a＜1，以AB为一边在圆O内作正△ABC，点D为圆O上不同于点A的一点，且DB=AB=a，DC的延长线交圆O于点E，则AE的长为（ ）
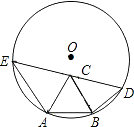A、 B、1 C、 D、a6. 已知点A，B，C在⊙O上（点C不与A，B重合）， ， 则 = °.7. 如图，在⊙O上依次取点A、B、C、D、E，测得∠A+∠C=220°，F为⊙O上异于E、D的一动点，则∠EFD= ．
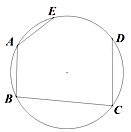8. ⊙C经过坐标原点，且与两坐标轴分别交于点A、B，点A的坐标为 ，M是圆上一点，∠BMO=150°.则圆心C的坐标为 ．
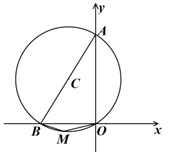9. 如图，已知 为四边形 的外接圆， 为圆心，若 BCD=120 º ，AB=AD=2cm，则 的半径长为 cm.
10. 如图，⊙ 的内接四边形ABCD两组对边的延长线分别相交于点E、F。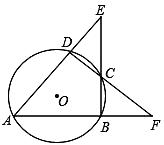
(1)、若∠E=∠F时，求证：∠ADC=∠ABC；(2)、若∠E=∠F=42°时，求∠A的度数；(3)、若∠E=α，∠F=β，且。α≠β.请你用含有α、β的代数式表示∠A的大小.11. 我们把有两条边和其中一边的对角对应相等的两个三角形叫做友好三角形。如图，在△ABC和△ABD中，AB=AB，AD=AC，∠ABC=∠ABD，则△ABC和△ABD是友好三角形。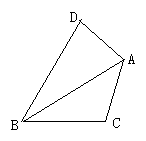
(1)、如图1，已知AD=AC，请写出图中的友好三角形；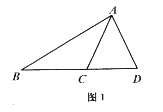
(2)、如图2，在△ABC和△ABD中，AD=AC，∠BDA=∠BCA，且∠BDA>90°，求证：△ABC≌△ABD；
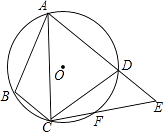
(3)、如图3，△ABC内接于圆，∠ABC=30°，∠BAC=45°，BC=4。D是圆上一点，若△ABD和△ABC是友好三角形，且BD<AD，求AD的长。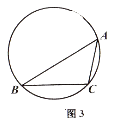
12. 定义：有一个角是其对角一半的圆的内接四边形叫做圆美四边形，其中这个角叫做美角．(1)、如图1，若四边形ABCD是圆美四边形，求美角∠A的度数．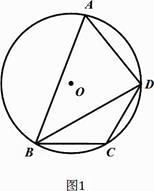
(2)、在(1)的条件下，若⊙O的半径为5．①求BD的长．
②如图2，在四边形ABCD中，若CA平分∠BCD，则BC+CD的最大值是 ．
(3)、在(1)的条件下，如图3，若AC是⊙O的直径，请用等式表示线段AB，BC，CD之间的数量关系，并说明理由．
二、中考演练
-
13. 如图，点 为线段 的中点，点 ， ， 到点 的距离相等，若 ，则 的度数是（ ）
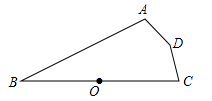A、 B、 C、 D、
