初中数学浙教版九年级上册3.5 圆周角 强化提升训练
试卷更新日期:2019-09-19 类型:同步测试
一、综合提升
-
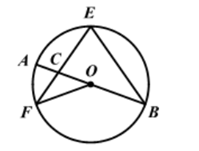
1. 如图,C,D是以线段AB为直径的⊙O上两点(位于AB两侧),CD=AD,且∠ABC=70°,则∠BAD的度数是( )
 A、50° B、45° C、35° D、30°2. 如图,在△ABC中,以边BC为直径做半圆,交AB于点D,交AC于点E,连接DE,若 =2 =2 ,则下外说法正确的是( )
A、50° B、45° C、35° D、30°2. 如图,在△ABC中,以边BC为直径做半圆,交AB于点D,交AC于点E,连接DE,若 =2 =2 ,则下外说法正确的是( )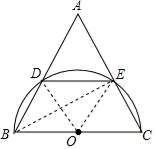 A、AB= AE B、AB=2AE C、3∠A=2∠C D、5∠A=3∠C3. 如图, 中, 是 内部的一个动点,且满足 ,则线段 长的最小值为( )
A、AB= AE B、AB=2AE C、3∠A=2∠C D、5∠A=3∠C3. 如图, 中, 是 内部的一个动点,且满足 ,则线段 长的最小值为( )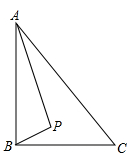 A、 B、 C、 D、4. 如图,AB是半圆O的直径,点D在半圆O上,AB= ,AD=10,C是弧BD上的一个动点,连接AC,过D点作DH⊥AC于H,连接BH,在点C移动的过程中,BH的最小值是( )
A、 B、 C、 D、4. 如图,AB是半圆O的直径,点D在半圆O上,AB= ,AD=10,C是弧BD上的一个动点,连接AC,过D点作DH⊥AC于H,连接BH,在点C移动的过程中,BH的最小值是( )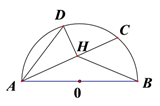 A、5 B、6 C、7 D、85. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A、5 B、6 C、7 D、85. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( ) A、2 B、8 C、 D、26. 如图,线段AB是⊙O的直径,点C在圆上,∠AOC=80°,点P是线段AB延长线上的一动点,连接PC,则∠APC的度数是度(写出一个即可).
A、2 B、8 C、 D、26. 如图,线段AB是⊙O的直径,点C在圆上,∠AOC=80°,点P是线段AB延长线上的一动点,连接PC,则∠APC的度数是度(写出一个即可). 7. 如图,⊙O的直径AB=8,P为O0上任一点(不同于A、B两点),∠APB的平分线交⊙O于点C,弦EF经过AC、BC的中点M、N,则弦EF的长为.
7. 如图,⊙O的直径AB=8,P为O0上任一点(不同于A、B两点),∠APB的平分线交⊙O于点C,弦EF经过AC、BC的中点M、N,则弦EF的长为.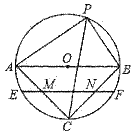 8. 如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G,连接DG.点E从点C运动到点D的过程中,DG的最小值为 .
8. 如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G,连接DG.点E从点C运动到点D的过程中,DG的最小值为 .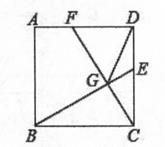 9. 定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.
9. 定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.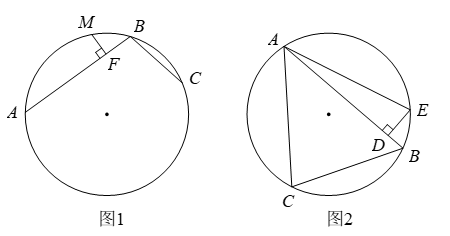
阿基米德折弦定理:如图1, 和 组成圆的折弦, , 是弧 的中点, 于 ,则 .
如图2,△ 中, , , , 是 上一点, ,作 交△ 的外接圆于 ,连接 ,则 =°.
10. 如图,AB、CD是⊙O的直径,DF、BE是弦,且DF=BE,求证:∠D=∠B.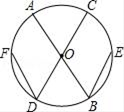 11. 已知:如图,⊙O1和⊙O2相交于A、B两点,动点P在⊙O2上,且在⊙1外,直线PA、PB分别交⊙O1于C、D,问:⊙O1的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明.
11. 已知:如图,⊙O1和⊙O2相交于A、B两点,动点P在⊙O2上,且在⊙1外,直线PA、PB分别交⊙O1于C、D,问:⊙O1的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明.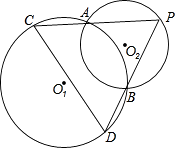 12. 如图,已知AB是半圆O的直径,OC⊥AB交半圆于点C,D是射线OC上一点,连结AD交半圆O于点E,连结BE,CE.
12. 如图,已知AB是半圆O的直径,OC⊥AB交半圆于点C,D是射线OC上一点,连结AD交半圆O于点E,连结BE,CE.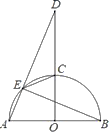 (1)、求证:EC平分∠BED.(2)、当EB=ED时,求证:AE=CE.
(1)、求证:EC平分∠BED.(2)、当EB=ED时,求证:AE=CE.二、中考演练
-
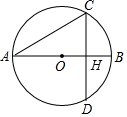
13. 如图所示,AB是⊙O的直径,弦 于H, ,则⊙O的半径是 .
 14. 如图, 是⊙ 上的四点,且点 是 的中点, 交 于点 , , ,那么 .
14. 如图, 是⊙ 上的四点,且点 是 的中点, 交 于点 , , ,那么 .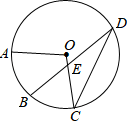 15. 如图, 是半圆 的直径, , 是 上两点,连接 , 并延长交于点 ,连接 , ,如果 ,那么 的度数为( )
15. 如图, 是半圆 的直径, , 是 上两点,连接 , 并延长交于点 ,连接 , ,如果 ,那么 的度数为( )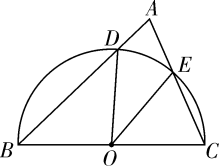 A、 B、 C、 D、16. 如图, 是 的弦, 交 于点 ,点 是 上一点, ,则 的度数为( ).
A、 B、 C、 D、16. 如图, 是 的弦, 交 于点 ,点 是 上一点, ,则 的度数为( ).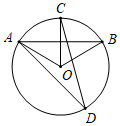 A、30° B、40° C、50° D、60°
A、30° B、40° C、50° D、60°