新人教版数学九年级上册24.4弧长和扇形的面积课时练习
试卷更新日期：2016-01-12 类型：同步测试
一、单选题
-
1.
如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠B=135°，则弧AC的长（ ）.
A、2π B、π C、 D、2.如图，扇形AOB中，∠AOB=150°，AC=AO=6，D为AC的中点，当弦AC沿扇形运动时，点D所经过的路程为（ ）
A、3π B、
C、
D、4π
3.如图，已知▱ABCD的对角线BD=4cm，将▱ABCD绕其对称中心O旋转180°，则点D所转过的路径长为（ ）
A、4π cm B、3π cm C、2π cm D、π cm4.如图，△ABC是等边三角形，AC=6，以点A为圆心，AB长为半径画弧DE，若∠1=∠2，则弧DE的长为（ ）
A、1π B、1.5π C、2π D、3π5.如图，点A、B、C都在⊙O上，⊙O的半径为2，∠ACB=30°，则弧AB的长是（ ）。
A、2π B、π C、 D、
6. 扇形的半径为30cm，圆心角为120°，此扇形的弧长是（ ）.A、20πcm B、10πcm C、10cm D、20cm7.如图，半径为1的圆O与正五边形ABCDE相切于点A、C，劣弧AC的长度为（ ）.
A、
B、
C、
D、
8.如图，正方形ABCD的边长为1，分别以顶点A、B、C、D为圆心，1为半径画弧，四条弧交于点E、F、G、H，则图中阴影部分的外围周长为（ ）
A、 B、 C、π D、π9.如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD=2 则阴影部分图形的面积为（ ）
A、4π B、2π C、π D、10. 如图，某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心，AB为半径的扇形（忽略铁丝的粗细），则所得扇形DAB的面积为（ ）
A、6 B、7 C、8 D、911.如图，直径AB为6的半圆，绕A点逆时针旋转60°，此时点B到了点B′，则图中阴影部分的面积是（ ）
A、3π B、6π C、5π D、4π12.如图，AB是⊙O的直径，点E为BC的中点，AB=4，∠BED=120°，则图中阴影部分的面积之和为（ ）.
A、 B、2 C、 D、113.一个扇形的半径为8cm，弧长为
πcm，则扇形的圆心角为（ ）A、60° B、120° C、150° D、180°14.如图，⊙O的半径为1，A、B、C是圆周上的三点，∠BAC=36°，则劣弧BC的长是（ ）
A、
B、
C、
D、
15.如图，正方形ABCD中，分别以B、D为圆心，以正方形的边长a为半径画弧，形成树叶形（阴影部分）图案，则树叶形图案的周长为（ ）
A、 B、
C、
D、3a
二、填空题
-
16.
如图，点A、B、C在半径为9的⊙O上， 弧AB的长为2π ， 则∠ACB的大小是.
17.如图，边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上．若∠BAD=120°，则弧BC的长度等于 .
18.如图，正六边形ABCDEF内接于⊙O，⊙O的半径为1，则弧AB的长为 .
19. 边长为4cm的正方形ABCD绕它的顶点A旋转180°，顶点B所经过的路线长为 cm．20. 在Rt△ABC中，斜边AB=4，∠B=60°，将△ABC绕点B旋转60°，顶点C运动的路线长是 （结果保留π）．三、解答题
-
21.
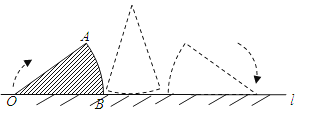
如图，在扇形纸片AOB中，OA=10，∠AOB=36°，OB在桌面内的直线l上．现将此扇形沿l按顺时针方向旋转（旋转过程中无滑动），当OA落在l上时，停止旋转．求点O所经过的路线长。
22.如图，⊙半径是1，A、B、C是圆周上的三点，∠BAC=36°，求劣弧BC的长
