初中数学浙教版九年级上册3.4 圆心角 强化提升训练
试卷更新日期:2019-09-19 类型:同步测试
一、综合提升
-
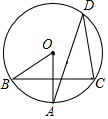
1. 如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
 A、6 B、8 C、5 D、52. 如图,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论中不正确的是( )
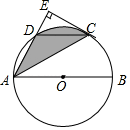
A、6 B、8 C、5 D、52. 如图,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论中不正确的是( )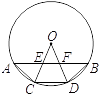 A、OE=OF B、弧AC=弧BD C、AC=CD=DB D、CD∥AB3. 如图,AB和CD是⊙O的两条直径,弦DE∥AB,若∠DOE=40°的弧,则∠BOC=( )
A、OE=OF B、弧AC=弧BD C、AC=CD=DB D、CD∥AB3. 如图,AB和CD是⊙O的两条直径,弦DE∥AB,若∠DOE=40°的弧,则∠BOC=( )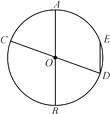 A、110° B、80° C、40° D、70°4. 如图,已知AB和CD是⊙O的两条等弦.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:①;②OM=ON;③PA=PC;④∠BPO=∠DPO,正确的个数是( )
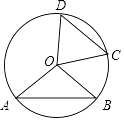
A、110° B、80° C、40° D、70°4. 如图,已知AB和CD是⊙O的两条等弦.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:①;②OM=ON;③PA=PC;④∠BPO=∠DPO,正确的个数是( )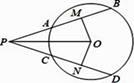 A、1 B、2 C、3 D、45. 如图, , , 是 的三等分点, 分别交 , 于点 , ,则下列结论正确的个数有( )
A、1 B、2 C、3 D、45. 如图, , , 是 的三等分点, 分别交 , 于点 , ,则下列结论正确的个数有( )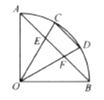
① ; ② ;
③ ; ④ .
A、1个 B、2个 C、3个 D、4个6. 如图,在半径为5cm的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为.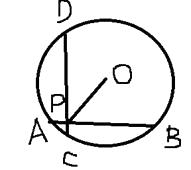 7. 如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C、D.若 ,则∠P的大小为度.
7. 如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C、D.若 ,则∠P的大小为度. 8. 如图,MN是⊙O的直径,OM=2,点A在⊙O上, ,B为弧AN的中点, P是直径MN上一动点,则PA+PB的最小值为 .
8. 如图,MN是⊙O的直径,OM=2,点A在⊙O上, ,B为弧AN的中点, P是直径MN上一动点,则PA+PB的最小值为 .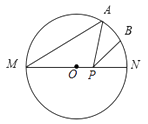 9. 如图,已知AB是⊙O的直径,C、D、E、F、G是 上的点,且有 ,则∠OCG= .
9. 如图,已知AB是⊙O的直径,C、D、E、F、G是 上的点,且有 ,则∠OCG= . 10. 如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN=cm.
10. 如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN=cm.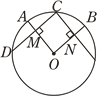 11. 如图,在⊙O中,C,D分别是OA,OB的中点,MC⊥AB,ND⊥AB,M,N在⊙O上.下列结论:①MC=ND;② ;③四边形MCDN是正方形;④MN= AB,其中正确的结论是(填序号).
11. 如图,在⊙O中,C,D分别是OA,OB的中点,MC⊥AB,ND⊥AB,M,N在⊙O上.下列结论:①MC=ND;② ;③四边形MCDN是正方形;④MN= AB,其中正确的结论是(填序号). 12. 如图,∠AOB=90°,C、D是弧AB的三等分点,AB分别交OC、OD于点E、F,求证:AE=BF=CD.
12. 如图,∠AOB=90°,C、D是弧AB的三等分点,AB分别交OC、OD于点E、F,求证:AE=BF=CD.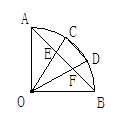 13. 如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.
13. 如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.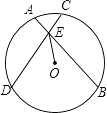 (1)、求证:AB=CD;(2)、若∠BED=60°,EO=2,求DE﹣AE的值.14. 如图, 的半径为5,弦 于E, .
(1)、求证:AB=CD;(2)、若∠BED=60°,EO=2,求DE﹣AE的值.14. 如图, 的半径为5,弦 于E, . (1)、求证: ;(2)、若 于F, 于G,试说明四边形OFEG是正方形.
(1)、求证: ;(2)、若 于F, 于G,试说明四边形OFEG是正方形.二、中考演练
-
15. 下列命题:①直线外一点到这条直线的垂线段,叫做点到直线的距离;②两点之间线段最短;③相等的圆心角所对的弧相等;④平分弦的直径垂直于弦.其中,真命题的个数是( )A、1 B、2 C、3 D、4