初中数学浙教版九年级上册3.4 圆心角 基础巩固训练
试卷更新日期:2019-09-19 类型:同步测试
一、单选题
-
1. 下列说法中,正确的是( )
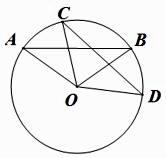
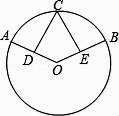
A、等弦所对的弧相等 B、等弧所对的弦相等 C、圆心角相等,所对的弦相等 D、弦相等所对的圆心角相等2. 如果两条弦相等,那么( )A、这两条弦所对的圆心角相等 B、这两条弦所对的弧相等 C、这两条弦所对的弦心距相等 D、以上说法都不对3. 将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,则这个扇形圆心角的度数为( )A、30°,60°,90° B、60°,120°,180° C、50°,100°,150° D、80°,120°,160°4. 已知AB、CD是两个不同圆的弦,如AB=CD,那么 与 的关系是( )A、 = B、 > C、 < D、不能确定5. 如图,已知AB是☉O的直径,D,C是劣弧EB的三等分点,∠BOC=40°,那么∠AOE=( ) A、40° B、60° C、80° D、120°6. 如图,已知AB是⊙O的直径,∠CBA=25°,则∠D的度数为( )
A、40° B、60° C、80° D、120°6. 如图,已知AB是⊙O的直径,∠CBA=25°,则∠D的度数为( )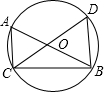 A、
A、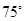 B、
B、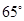 C、
C、 D、
D、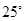 7. 已知,如图, ,下列结论不一定成立的是( )
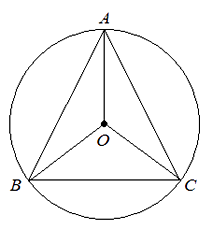
7. 已知,如图, ,下列结论不一定成立的是( ) A、 B、 C、 D、 、 都是等边三角形
A、 B、 C、 D、 、 都是等边三角形二、填空题
-
8. 在半径为R的⊙O中,有一条弦等于半径,则弦所对的圆心角为.
9. 一条弦把圆分为2∶3的两部分,那么这条弦所对的圆周角度数为。10. 如图,已知AB,CD是☉O的直径, = ,∠AOE=32°,那么∠COE的度数为度.