初中数学浙教版九年级上册3.2 图形的旋转 强化提升训练
试卷更新日期:2019-09-19 类型:同步测试
一、综合提升
-
1. 如图所示,可以看作是正方形ABCD绕点O分别旋转多少度前后的图形共同组成的( )
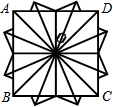 A、30°,45° B、60°,45° C、45°,90° D、22.5°,67.5°2. 如图,▱ABCD绕点A逆时针旋转30°,得到▱AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )
A、30°,45° B、60°,45° C、45°,90° D、22.5°,67.5°2. 如图,▱ABCD绕点A逆时针旋转30°,得到▱AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( ) A、105° B、170° C、155° D、145°3. 如图,△ABC中,∠A=75°,∠B=50°,将△ABC绕点C按逆时针方向旋转,得到△A’B’ C,点A的对应点A'落在AB边上,则∠BCA'的度数为( )
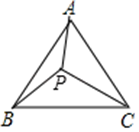
A、105° B、170° C、155° D、145°3. 如图,△ABC中,∠A=75°,∠B=50°,将△ABC绕点C按逆时针方向旋转,得到△A’B’ C,点A的对应点A'落在AB边上,则∠BCA'的度数为( )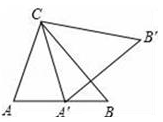 A、20° B、25° C、30° D、35°4. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB'C'(点B的对应点是点B',点C的对应点是点C'),连接CC',若∠B=78°,则∠CC'B'的大小是( )
A、20° B、25° C、30° D、35°4. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB'C'(点B的对应点是点B',点C的对应点是点C'),连接CC',若∠B=78°,则∠CC'B'的大小是( )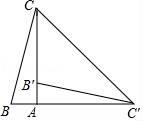 A、23° B、30° C、33° D、39°5. 如图在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…若点A( ,0),B(0,2),则点B2018的坐标为( )
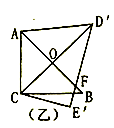
A、23° B、30° C、33° D、39°5. 如图在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…若点A( ,0),B(0,2),则点B2018的坐标为( )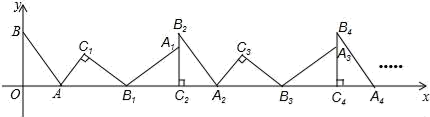 A、(6048,0) B、(6054,0) C、(6048,2) D、(6054,2)6. 如图,把一副三角板如图甲放置,其中 ,斜边 ,把三角板 绕点 顺时针旋转 得到 (如图乙).这时 与 相交于点 , 与 相交于点 ,则 的度数为.
A、(6048,0) B、(6054,0) C、(6048,2) D、(6054,2)6. 如图,把一副三角板如图甲放置,其中 ,斜边 ,把三角板 绕点 顺时针旋转 得到 (如图乙).这时 与 相交于点 , 与 相交于点 ,则 的度数为.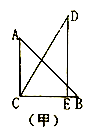
 7. 如图,在平面直角坐标系 中,点 , 分别在 轴、 轴上, . 先将线段 沿 轴翻折得到线段 ,再将线段 绕点 顺时针旋转30°得到线段 ,连接 . 若点 的坐标为 ,则线段 的长为.
7. 如图,在平面直角坐标系 中,点 , 分别在 轴、 轴上, . 先将线段 沿 轴翻折得到线段 ,再将线段 绕点 顺时针旋转30°得到线段 ,连接 . 若点 的坐标为 ,则线段 的长为.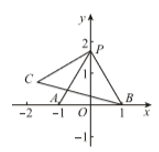 8. 如图,在△AOB和△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为.
8. 如图,在△AOB和△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为.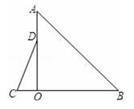 9. 将两块全等的直角三角板按如图方式放置, ,固定三角板 ,然后将三角板 绕点 顺时针旋转到如图的位置,此时 与 , 分别交于点 , , 与 交于点 ,且 ,则旋转角的度数为 .
9. 将两块全等的直角三角板按如图方式放置, ,固定三角板 ,然后将三角板 绕点 顺时针旋转到如图的位置,此时 与 , 分别交于点 , , 与 交于点 ,且 ,则旋转角的度数为 .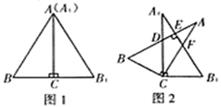 10. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, 的顶点均在格点上,点 的坐标为 .
10. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, 的顶点均在格点上,点 的坐标为 .
①把 向上平移5个单位后得到对应的 ,画出 ,并写出 的坐标;
②以原点. .为对称中心,画出 与关于原点. .对称的 ,并写出点 的坐标.
③以原点O为旋转中心,画出把 顺时针旋转90°的图形△A3B3C3 , 并写出C3的坐标.
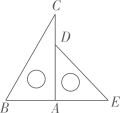
11. 如图,点A′在Rt△ABC的边AB上,∠ABC=30°,AC=2,∠ACB=90°,△ACB绕顶点C按逆时针方向旋转与△A′CB′重合,A'B'与BC交于点D,连接BB′,求线段BB′的长度.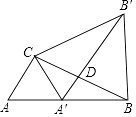 12. 一副三角板OAC、OBD如图(1)放置,(∠BDO=30°、∠CAO=45°)
12. 一副三角板OAC、OBD如图(1)放置,(∠BDO=30°、∠CAO=45°) (1)、若OM、ON分别平分∠BOA、∠DOC,求∠MON的度数;(2)、将三角板OBD从图(1)绕O点顺时针旋转如图(2),若OM、ON分别平分∠BOA、∠DOC,则在旋转过程中∠MON如何变化?(3)、若三角板OBD从图(1)绕O点逆时针旋转如图(3),若其它条件不变,则(2)的结论是否成立?(4)、若三角板OBD从图(1)绕O点逆时针旋转,其它条件不变,在旋转过程中,∠MON是否一直不变,在备用图中画图说明.
(1)、若OM、ON分别平分∠BOA、∠DOC,求∠MON的度数;(2)、将三角板OBD从图(1)绕O点顺时针旋转如图(2),若OM、ON分别平分∠BOA、∠DOC,则在旋转过程中∠MON如何变化?(3)、若三角板OBD从图(1)绕O点逆时针旋转如图(3),若其它条件不变,则(2)的结论是否成立?(4)、若三角板OBD从图(1)绕O点逆时针旋转,其它条件不变,在旋转过程中,∠MON是否一直不变,在备用图中画图说明.二、中考演练
-
13. 如图,△A′B′C′是由△ABC经过平移得到的,△A′B′C′还可以看作是△ABC经过怎样的图形变化得到?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )
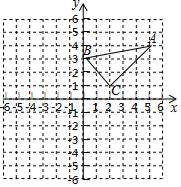
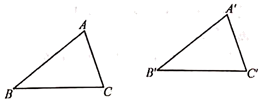 A、①④ B、②③ C、②④ D、③④14. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点 的坐标是( )
A、①④ B、②③ C、②④ D、③④14. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点 的坐标是( )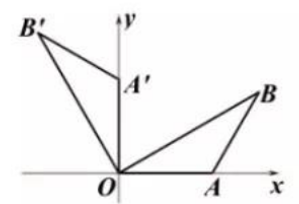 A、 B、 C、 D、15. 如图,将 的斜边AB绕点A顺时针旋转 得到AE,直角边AC绕点A逆时针旋转 得到AF,连结EF.若 , ,且 ,则 .
A、 B、 C、 D、15. 如图,将 的斜边AB绕点A顺时针旋转 得到AE,直角边AC绕点A逆时针旋转 得到AF,连结EF.若 , ,且 ,则 .