初中数学浙教版九年级上册3.2 图形的旋转 基础巩固训练
试卷更新日期:2019-09-19 类型:同步测试
一、旋转现象
-
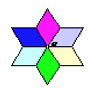
1. 下列现象:①时针转动;②荡秋千;③转呼啦圈;④传送带上电视机的运动.其中属于旋转的有( )A、①② B、②③ C、①④ D、③④2. 将下列图形绕着直线旋转一周正好得到如图所示的图形的是( )
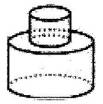 A、
A、 B、
B、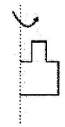 C、
C、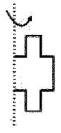 D、
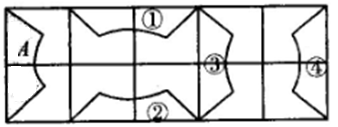
D、 3. 视力表的一部分如图,其中开口向上的两个“E”之间的变换是( )
3. 视力表的一部分如图,其中开口向上的两个“E”之间的变换是( ) A、平移 B、旋转 C、对称 D、都不对4. 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,将△ADE顺时针旋转90°后得到的图形是( )
A、平移 B、旋转 C、对称 D、都不对4. 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,将△ADE顺时针旋转90°后得到的图形是( ) A、
A、 B、
B、 C、
C、 D、
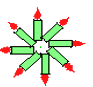
D、 5. 如图,把这个“十字星”形图绕其中心点O旋转,当至少旋转度后,所得图形与原图形重合.
5. 如图,把这个“十字星”形图绕其中心点O旋转,当至少旋转度后,所得图形与原图形重合.
二、旋转的性质
-
6. 如图,扎西坐在旋转的秋千上,请在图中画出点A,B,C的对应点A' , B' , C'.
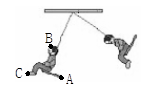 7. 如图,将△ABC绕点A旋转后得到△ADE,则旋转方式是( )
7. 如图,将△ABC绕点A旋转后得到△ADE,则旋转方式是( )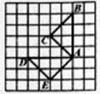 A、逆时针旋转90° B、顺时针旋转90° C、顺时针旋转45° D、逆吋针旋转45°8. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是( )
A、逆时针旋转90° B、顺时针旋转90° C、顺时针旋转45° D、逆吋针旋转45°8. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是( ) A、25° B、30° C、35° D、40°9. 如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC绕某点逆时针旋转后能与△BAD重合,问:
A、25° B、30° C、35° D、40°9. 如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC绕某点逆时针旋转后能与△BAD重合,问: (1)、旋转中心是;(2)、逆时针旋转度;(3)、若EC=10cm,则BD的长度是cm.10. 如图,将△ABC绕点C顺时针方向旋转40°得△A′B′C′,若AC⊥A′B′,求∠BAC的度数.
(1)、旋转中心是;(2)、逆时针旋转度;(3)、若EC=10cm,则BD的长度是cm.10. 如图,将△ABC绕点C顺时针方向旋转40°得△A′B′C′,若AC⊥A′B′,求∠BAC的度数. 11. 如图所示,将△ABC绕其顶点A顺时针旋转30°后得△ADE.
11. 如图所示,将△ABC绕其顶点A顺时针旋转30°后得△ADE.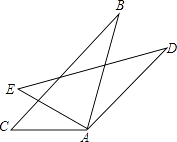 (1)、问△ABC与△ADE的关系如何?
(1)、问△ABC与△ADE的关系如何?
(2)、求∠BAD的度数.三、旋转-坐标与图形变化
-
12. 如图,在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA',则点A'的坐标是( )
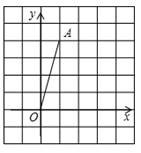 A、(1,4) B、(4,1) C、(4,-1) D、(2,3)13. 在平面直角坐标系xOy中,已知点A(2,3).若将OA绕原点O逆时针旋转180°得到OA’,则点A’在平面直角坐标系中的位置是在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限14. 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形)。其中A(1,1)、B(4,4)、C(5,1).
A、(1,4) B、(4,1) C、(4,-1) D、(2,3)13. 在平面直角坐标系xOy中,已知点A(2,3).若将OA绕原点O逆时针旋转180°得到OA’,则点A’在平面直角坐标系中的位置是在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限14. 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形)。其中A(1,1)、B(4,4)、C(5,1).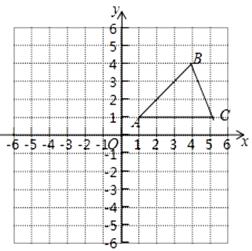 (1)、将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;(2)、将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△A2B2C2 , A、B、C的对应点分别是A2、B2、C2;(3)、连CB2 , 直接写出点B2、C2的坐标B2:、C2: .
(1)、将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;(2)、将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△A2B2C2 , A、B、C的对应点分别是A2、B2、C2;(3)、连CB2 , 直接写出点B2、C2的坐标B2:、C2: .四、利用旋转进行图形设计