新人教版数学九年级上册第二十二章第一节二次函数的图象和性质同步训练
试卷更新日期:2016-01-11 类型:同步测试
一、单选题
-
1.
抛物线 的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为 ,则b、c的值为( ).
A、b=2, c=-6 B、b=2, c=0 C、b=-6, c=8 D、b=-6, c=22.已知抛物线 过A(-2,0),O(0,0),B(-3,y1),C(3,y2)四点,则y1与y2大小关系是( )
A、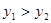 B、
C、
D、不能确定
3.
B、
C、
D、不能确定
3.已知
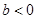 ,二次函数
,二次函数 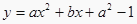 的图象为下列四个图象之一,试根据图象分析a的值应等于( ).
的图象为下列四个图象之一,试根据图象分析a的值应等于( ).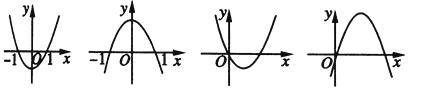 A、-2 B、-1 C、1 D、24. 已知二次函数y=ax2﹣2x+2(a>0),那么它的图象一定不经过( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 抛物线y=2x2 , y=﹣2x2 , y=x2共有的性质是( )
A、-2 B、-1 C、1 D、24. 已知二次函数y=ax2﹣2x+2(a>0),那么它的图象一定不经过( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 抛物线y=2x2 , y=﹣2x2 , y=x2共有的性质是( )
A、开口向下 B、对称轴是y轴 C、都有最低点 D、y的值随x的增大而减小6. 抛物线y=2x2+1的顶点坐标是( )
A、(2,1) B、(0,1) C、(1,0) D、(1,2)7. 对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )
A、开口向下 B、对称轴是x=﹣1 C、顶点坐标是(1,2) D、与x轴有两个点8. 已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是( )
A、6 B、5 C、4 D、39. 抛物线y=(x﹣1)2﹣3的对称轴是( )
A、y轴 B、直线x=﹣1 C、直线x=1 D、直线x=﹣310. 下列函数是二次函数的是( )A、y=2(x-2)2-2x2 B、y =ax2+bx+c C、 D、y= (x-2)2+111.抛物线 , ,
 的图象开口最大的是( )A、 B、y= -3x2 C、y=2x2 D、不确定12. 函数y=ax2(a≠0)的图象与a的符号有关的是( )A、对称轴 B、顶点坐标 C、开口方向 D、开口大小13. 下列各点中与点(1,4)在同一个二次函数y=ax2图象上的是( )A、(2,-16) B、( -2,16) C、(-2,-16) D、(16,2)14.
的图象开口最大的是( )A、 B、y= -3x2 C、y=2x2 D、不确定12. 函数y=ax2(a≠0)的图象与a的符号有关的是( )A、对称轴 B、顶点坐标 C、开口方向 D、开口大小13. 下列各点中与点(1,4)在同一个二次函数y=ax2图象上的是( )A、(2,-16) B、( -2,16) C、(-2,-16) D、(16,2)14.抛物线 的顶点在( )
A、第一象限 B、第二象限 C、 轴上
D、
轴上
D、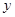 轴上
15. 已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )A、
轴上
15. 已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )A、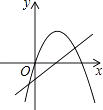 B、
B、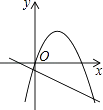 C、
C、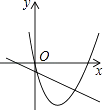 D、
D、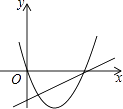
二、填空题
-
16.
点A(2,y1)、B(3,y2)是二次函数
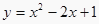 的图象上两点,则y1与y2大小关系为y1 y2(填“>”“<”“=”)17. 二次函数y=ax2+4x+a的最大值是3,则a= .18. 将抛物线y=2x2先向右平移3个单位,再向下平移2个单位,所得到的抛物线的关系式为.19. 抛物线y=2(x-3)2-5的开口方向是;对称轴;顶点坐标是 .20. 抛物线y=0.5(x+4)2+2,当x=时,y有最值,值为.
的图象上两点,则y1与y2大小关系为y1 y2(填“>”“<”“=”)17. 二次函数y=ax2+4x+a的最大值是3,则a= .18. 将抛物线y=2x2先向右平移3个单位,再向下平移2个单位,所得到的抛物线的关系式为.19. 抛物线y=2(x-3)2-5的开口方向是;对称轴;顶点坐标是 .20. 抛物线y=0.5(x+4)2+2,当x=时,y有最值,值为.三、解答题
-
21. 已知二次函数图象的顶点坐标为(1,-1),且经过原点(0,0),求该函数的解析式.22.
如图,已知二次函数 的图象经过A(2,0)、B(0,-6)两点.
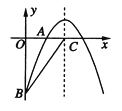 (1)、求这个二次函数的解析式;(2)、设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
(1)、求这个二次函数的解析式;(2)、设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.