新人教版数学九年级上册第二十二章第一节二次函数y=ax²图象课时练习
试卷更新日期:2016-01-11 类型:同步测试
一、单选题
-
1. 若二次函数 的图象经过点P(-2,4),则该图象必经过点( )A、(2,4) B、(-2,-4) C、(-4,2) D、(4,-2)2. 如图所示的四个函数的图象分别对应的函数是① ;②
 ;③
;③  ;④ ,则a, b, c, d的大小关系为( )
;④ ,则a, b, c, d的大小关系为( )
 A、 B、
A、 B、 C、
D、
C、
D、 3.
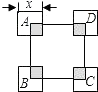
3.如图,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD各边平行或垂直.若小正方形的边长为x,且0<x≤10,阴影部分的面积为y,则能反映y与x之间函数关系的大致图象是( )
 A、
A、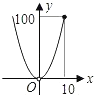 B、
B、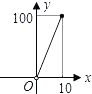 C、
C、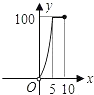 D、
D、 4. 关于函数 的性质的叙述,错误的是( )A、对称轴是y轴 B、顶点是原点 C、当x>0时,y随x的增大而增大 D、y有最大值5. 在同一坐标系中,抛物线 , , 的共同点是( )A、开口向上,对称轴是y轴,顶点是原点 B、对称轴是y轴,顶点是原点 C、开口向下,对称轴是y轴,顶点是原点 D、有最小值为06. 在同一平面直角坐标系中,同一水平线上开口最大的抛物线是( )A、 B、 C、
4. 关于函数 的性质的叙述,错误的是( )A、对称轴是y轴 B、顶点是原点 C、当x>0时,y随x的增大而增大 D、y有最大值5. 在同一坐标系中,抛物线 , , 的共同点是( )A、开口向上,对称轴是y轴,顶点是原点 B、对称轴是y轴,顶点是原点 C、开口向下,对称轴是y轴,顶点是原点 D、有最小值为06. 在同一平面直角坐标系中,同一水平线上开口最大的抛物线是( )A、 B、 C、 D、
7. 下列函数中,具有过原点,且当 时, 随 的增大而减小,这两个特征的有( )
D、
7. 下列函数中,具有过原点,且当 时, 随 的增大而减小,这两个特征的有( )①
 ②
② ③ ④
A、1个 B、2个 C、3个 D、4个8. 若对任意实数x,二次函数 的值总是非负数,则 a 的取值范围是( ) A、 B、
的值总是非负数,则 a 的取值范围是( ) A、 B、 C、
D、a<-1
9. 下列说法错误的是( )A、在二次函数 中,当 时, 随 的增大而增大 B、在二次函数 中,当 时, 有最大值 0 C、a 越大图象开口越小, a 越小图象开口越大 D、无论 a 是正数或负数, 的顶点一定是坐标原点10. 已知点A( , ),B( , ),C(2, )在抛物线 上,则 、 、 的大小关系是( )A、 B、 C、 D、11. 已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )A、
C、
D、a<-1
9. 下列说法错误的是( )A、在二次函数 中,当 时, 随 的增大而增大 B、在二次函数 中,当 时, 有最大值 0 C、a 越大图象开口越小, a 越小图象开口越大 D、无论 a 是正数或负数, 的顶点一定是坐标原点10. 已知点A( , ),B( , ),C(2, )在抛物线 上,则 、 、 的大小关系是( )A、 B、 C、 D、11. 已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )A、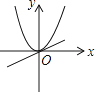 B、
B、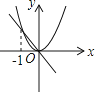 C、
C、 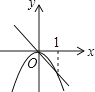 D、
D、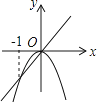 12. 函数y=ax2(a≠0)的图象与a的符号有关的是( )A、对称轴 B、顶点坐标 C、开口方向 D、开口大小13. 下列各点中与点(1,4)在同一个二次函数y=ax2图象上的是( )A、(2,-16) B、( -2,16) C、(-2,-16) D、(16,2)14. 下列函数中,当x>0时y随x的增大而减小的有( )A、 B、 C、 D、15. 抛物线 , , 的图象开口最小的是( )A、 B、y= -3x2 C、y=2x2 D、不确定;
12. 函数y=ax2(a≠0)的图象与a的符号有关的是( )A、对称轴 B、顶点坐标 C、开口方向 D、开口大小13. 下列各点中与点(1,4)在同一个二次函数y=ax2图象上的是( )A、(2,-16) B、( -2,16) C、(-2,-16) D、(16,2)14. 下列函数中,当x>0时y随x的增大而减小的有( )A、 B、 C、 D、15. 抛物线 , , 的图象开口最小的是( )A、 B、y= -3x2 C、y=2x2 D、不确定;二、填空题
-
16. 如果一个二次函数的图象开口向下,对称轴为y轴,顶点坐标为(0,0),试写出一个符合要求的函数解析式:.17. 已知A(-1,y1),B(-2,y2),C(3,y3)三点都在二次函数
 的图象上,则y1 , y2 , y3的大小关系是. 18. 已知二次函数 的图象开口向下,则m的值为.19. 若点A(1,n)在二次函数 的图象上,则点A关于抛物线对称轴的对称点 的坐标是 , 这两点间的线段被对称轴 .20. 若二次函数 的图象过点(1,-2),则 a 的值是 .
的图象上,则y1 , y2 , y3的大小关系是. 18. 已知二次函数 的图象开口向下,则m的值为.19. 若点A(1,n)在二次函数 的图象上,则点A关于抛物线对称轴的对称点 的坐标是 , 这两点间的线段被对称轴 .20. 若二次函数 的图象过点(1,-2),则 a 的值是 .三、解答题
-
21. 已知函数 是关于x的二次函数,求:(1)、满足条件的k的值;(2)、当k为何值时,抛物线有最高点?求出这个最高点;(3)、当k为何值时,函数有最小值?最小值是多少?
22. 二次函数 与直线 交于点P(1,b). (1)、求a、b的值;(2)、写出二次函数的关系式,并指出x取何值时,该函数的y随x的增大而减小.
交于点P(1,b). (1)、求a、b的值;(2)、写出二次函数的关系式,并指出x取何值时,该函数的y随x的增大而减小.
 过点( , )和点(1,6),
过点( , )和点(1,6),