河北省张家口市2018-2019学年高二文数12月月考试卷
试卷更新日期:2019-09-17 类型:月考试卷
一、单选题
-
1. 已知命题 所有的幂函数图象都过 ,则 为( )A、所有的幂函数图象都不过 B、所有的幂函数图象不都过 C、存在一个幂函数,它的图象不过 D、存在一个函数图象过 ,它不是幂函数2. 下列求导数运算正确的是( )A、 B、 C、 D、3. 设 ,则 是 的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要4. 抛物线 的焦点坐标为( )A、 B、 C、 D、5. 函数 的单调递减区间为( )A、 B、 C、 D、6. 命题 ,命题 函数 的最小值为2,给出下列命题:“ ”“ ”“ ”“ ”,其中真命题的个数为( )A、1 B、2 C、3 D、47. 中心在坐标原点,离心率为 的双曲线的焦点在 轴上,则它的渐近线方程为( )A、 B、 C、 D、8. 函数 在其定义域内可导,其图象如图所示, 则导函数 的图象可能为( )
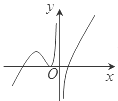 A、
A、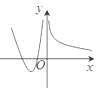 B、
B、 C、
C、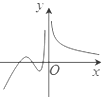 D、
D、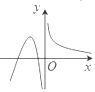 9. 已知双曲线 的离心率等于 ,直线 与双曲线的左右两支各有一个交点,则 的取值范围是( )A、 B、 C、 D、10. 执行如图所示的程序框图,若输入 ,则输出的 值为( )
9. 已知双曲线 的离心率等于 ,直线 与双曲线的左右两支各有一个交点,则 的取值范围是( )A、 B、 C、 D、10. 执行如图所示的程序框图,若输入 ,则输出的 值为( ) A、3 B、 C、 D、11. 已知椭圆 的左右顶点分别为 ,且以线段 为直径的圆与直线 相切,则 的离心率为( )A、 B、 C、 D、12. 已知函数 , ,若方程 在 有四个不同的解,则 的取值范围为( )A、 B、 C、 D、
A、3 B、 C、 D、11. 已知椭圆 的左右顶点分别为 ,且以线段 为直径的圆与直线 相切,则 的离心率为( )A、 B、 C、 D、12. 已知函数 , ,若方程 在 有四个不同的解,则 的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 书架上有2本不同的语文书,1本数学书,从中任意取出2本,取出的书恰好都是语文书的概率为 .14. 已知函数 既有极大值又有极小值,则实数 的取值范围是 .15. 动圆经过点 ,且与直线 相切,则动圆圆心 的轨迹方程为 .16. 已知函数 , ,当 时,函数 的图象始终在 图象的下方,则实数 的取值范围是 .
三、解答题
-
17. 已知双曲线 .(1)、求双曲线的右焦点到渐近线的距离;(2)、求与双曲线有共同渐近线,且过点 的双曲线的标准方程.18. 已知函数 在 处有极值1.(1)、求 的值;(2)、求函数 在 的值域.19. 命题 , 成立,命题 , 成立.(1)、若命题 为真命题,求实数 的取值范围;(2)、若命题 为真命题,求实数 的取值范围;(3)、若命题 为真命题,求实数 的取值范围.