海南省海口市2019年初中毕业生学业模拟考试数学试卷（一）

试卷更新日期：2019-09-17 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣ $\frac{1}{5}$ 的绝对值是（）

A、5 B、﹣5 C、 $\frac{1}{5}$ D、﹣ $\frac{1}{5}$

查看试题解析
2. 数据2060000000科学记数法表示为（）

A、206×10⁷ B、20.6×10⁸ C、2.06×10⁸ D、2.06×10⁹

查看试题解析
3. 满足 $\sqrt{5} < x < \sqrt{18}$ 的整数x的值是（）

A、3 B、4 C、2和3 D、3和4

查看试题解析
4. 若（）•（﹣xy）²＝4x²y³ ，则括号里应填的单项式是（）

A、﹣4y B、4y C、4xy D、﹣2xy

查看试题解析
5. 如图所示的几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
6. 一个多边形每个内角都是150°，则这个多边形的边数为（）

A、12 B、10 C、8 D、6

查看试题解析
7. 一家商店将某种服装按每件的成本价a元提高50%标价，又以8折优惠卖出，则这种服装每件的售价是（）

A、 $1.5 a$ 元 B、 $1.2 a$ 元 C、 $0.8 a$ 元 D、 $0.4 a$ 元

查看试题解析
8. 如图，直线a∥b，等边三角形ABC的顶点B在直线b上，若∠1＝34°，则∠2等于（）

A、84° B、86° C、94° D、96°

查看试题解析
9. 如图，AD是△ABC外接圆的直径.若∠B＝64°，则∠DAC等于（）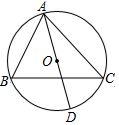

A、26° B、28° C、30° D、32°

查看试题解析
10. 如图，在菱形ABCD中，点E是BC的中点，DE与AC交于点F，若AB＝6，∠B＝60°，则AF的长为（）

A、3 B、3.5 C、3 $\sqrt{3}$ D、4

查看试题解析
11. 如图，直线l与x轴、y轴分别交于A、B两点，与反比例函数y＝ $\frac{k}{x}$ 的图象在第一象限相交于点C.若AB＝BC，△AOB的面积为3，则k的值为（）

A、6 B、9 C、12 D、18

查看试题解析
12. 如图，管中放置着三根同样的绳子AA₁、BB₁、CC₁小明和小张两人分别站在管的左右两边，各随机选该边的一根绳子，若每边每根绳子被选中的机会相等，则两人选到同根绳子的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{6}$ D、 $\frac{1}{9}$

查看试题解析

二、填空题

13. 化简 $\frac{2 a - 6}{a^{2} - 6 a + 9} =$ .

查看试题解析
14. 不等式组 ${\begin{array}{l} 2 x + 1 < - 1 \\ 3 - x > 1 \end{array}$ 的解集为.

查看试题解析
15. 如图，正方形ABCD的边长为4，G是BC边上一点.若矩形DEFG的边EF经过点A，GD＝5，则FG长为.

查看试题解析
16. 如图，△ABC中，∠ACB＝90°，AB＝5，AC＝3，BC为半圆O的直径，将△ABC沿射线CB方向平移得到△A₁B₁C₁.当A₁B₁与半圆O相切于点D时，平移的距离的长为.

查看试题解析

三、解答题

17.

(1)、计算： ${(- 1)}^{8} + 24 \times {(- 2)}^{- 3} - \frac{\sqrt{48}}{2 \sqrt{3}}$

(2)、解方程： $\frac{2}{x - 1} + \frac{x^{2}}{x^{2} - 1} = 1$

查看试题解析
18. 某商场用2500元购进A、B两种新型节能台灯共50盏，这两种台灯的进价、标价如下表所示.

类型

价格

A型

B型

进价（元/盏）

40

65

标价（元/盏）

60

100

(1)、这两种台灯各购进多少盏？

(2)、在每种台灯销售利润不变的情况下，若该商场计划销售这批台灯的总利润至少为1400元，问至少需购进B种台灯多少盏？

查看试题解析
19. 为了了解同学们对垃圾分类知识的了解程度，增强同学们的环保意识，某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷，并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况，将测试成绩分成A、B、C、D四组，绘制了如下统计图表：

组别

分数/分

A

60＜x≤70

B

70＜x≤80

C

80＜x≤90

D

90＜x≤100

请结合以上信息解答下列问题：

(1)、本次抽样调查的样本总量是多少？

(2)、样本中，测试成绩在B组的频数是多少，在D组的频率是多少？

(3)、样本中，这次测试成绩的中位数落在哪一组？

(4)、如果该校共有800名学生，请估计成绩在90＜x≤100的学生约有多少人？

查看试题解析
20.
如图1，某超市从底楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的坡度为1：2.4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，求二楼的层高BC（精确到0.1米）．
（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）

查看试题解析
21. 如图，在矩形ABCD中，AB＝4，BC＝5，E是BC边上的一个动点，DF⊥AE，垂足为点F，连结CF

(1)、若AE＝BC
①求证：△ABE≌△DFA；②求四边形CDFE的周长；③求tan∠FCE的值；

(2)、探究：当BE为何值时，△CDF是等腰三角形.

查看试题解析
22. 如图，对称轴为直线x＝1的抛物线经过A（﹣1，0）、C（0，3）两点，与x轴的另一个交点为B，点D在y轴上，且OB＝3OD

(1)、求该抛物线的表达式；

(2)、设该抛物线上的一个动点P的横坐标为t
①当0＜t＜3时，求四边形CDBP的面积S与t的函数关系式，并求出S的最大值；

②点Q在直线BC上，若以CD为边，点C、D、Q、P为顶点的四边形是平行四边形，请求出所有符合条件的点P的坐标.

查看试题解析

组别	分数/分
A	60＜x≤70
B	70＜x≤80
C	80＜x≤90
D	90＜x≤100