海南省定安县2019年数学中考一模试卷
试卷更新日期：2019-09-17 类型：中考模拟
一、单选题
-
1. 2019的倒数是（ ）A、2019 B、﹣2019 C、 D、﹣2. 函数y= 中自变量x的取值范围是（ ）A、 B、 C、 D、3. 小星同学在“百度”搜索引擎中输入“中国梦，我的梦”，能搜索到与之相关的结果的条数约为61700000，这个数用科学记数法表示为（ ）
A、617×105 B、6.17×106 C、6.17×107 D、0.617×1084. 如图由6个等大的小立方体搭成的，有关三视图的说法正确的是（ ）
A、正视图（主视图）面积最大 B、左视图面积最大 C、俯视图面积最大 D、三种视图面积一样大5. 不等式3x﹣1＞5的解集在数轴上表示正确的是（ ）A、
B、
C、
D、
6. 一组数据4，2，x，3，9的平均数为4，则这组数据的众数和中位数分别是（ ）A、3，2 B、2，2 C、2，3 D、2，47. 一次函数y＝（k﹣1）x+3的图象经过点（﹣2，1），则k的值是（ ）A、﹣1 B、2 C、1 D、08. 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（ ）A、
B、
C、
D、
9. 下列各图中，∠1＝∠2的图形的个数有（ ）
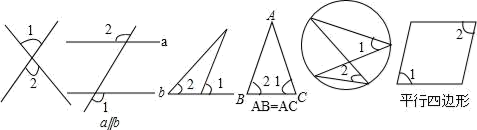A、3 B、4 C、5 D、610. 如图，直线l1 ， l2 ， l3交于一点，直线l4∥l1 ， 若∠1＝124°，2＝84°，则∠3的度数为（ ）
A、30° B、40° C、45° D、60°11. 如图，⊙A过点O（0，0），C（ ，0），D（0，1），点B是x轴下方⊙A上的一点，连接BO，BD，则∠OBD的度数是（ ）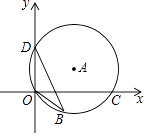
A、15° B、30° C、45° D、60°12. 如图，E为矩形ABCD的边AB上一点，将矩形沿CE折叠，使点B恰好落在ED上的点F处，若BE=1，BC=3，则CD的长为（ ）
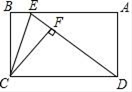A、6 B、5 C、4 D、3二、填空题
-
13. 若 ＝ ，则 的值为.14. 分式方程 的根为.15. 在一个不透明的盒子中有12个白球，若干个黄球，它们除了颜色不同外，其余均相同，若从中随机摸出一个球是黄球的概率是 ，则黄球的个数.16. 如图，边长为1的小正方形构成的网格中，半径为1的⊙O在格点上，则∠AED的正切值为.
三、解答题
-
17.(1)、计算：（﹣2）2× ﹣（ ）﹣2；(2)、化简求值：2a（1﹣2a）+（2a+1）（2a﹣1），其中a＝2.18. 根据图中给出的信息，解答下列问题：
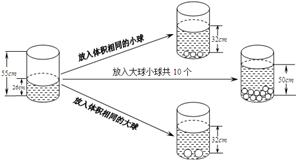(1)、放入一个小球水面升高， ，放入一个大球水面升高 ；(2)、如果要使水面上升到50 ，应放入大球、小球各多少个？19. 定安县定安中学初中部三名学生竞选校学生会主席，他们的笔试成绩和演讲成绩（单位：分）分别用两种方式进行统计，如表和图.A
B
C
笔试
85
95
90
口试
80
85
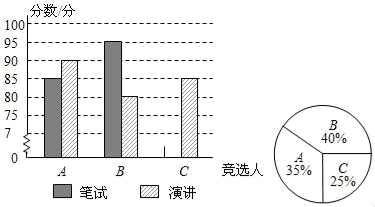(1)、请将表和图中的空缺部分补充完整；(2)、图中B同学对应的扇形圆心角为度；(3)、竞选的最后一个程序是由初中部的300名学生进行投票，三名候选人的得票情况如图（没有弃权票，每名学生只能推荐一人），则A同学得票数为 ， B同学得票数为 ， C同学得票数为；(4)、若每票计1分，学校将笔试、演讲、得票三项得分按4：3：3的比例确定个人成绩，请计算三名候选人的最终成绩，并根据成绩判断当选.（从A，B，C选择一个填空）20. 如图，在大楼AB的正前方有一斜坡CD，CD=13米，坡比DE：EC=1： ，高为DE，在斜坡下的点C处测得楼顶B的仰角为64°，在斜坡上的点D处测得楼顶B的仰角为45°，其中A、C、E在同一直线上.
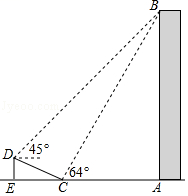(1)、求斜坡CD的高度DE；(2)、求大楼AB的高度；（参考数据：sin64°≈0.9，tan64°≈2）.21. 如图1，在正方形ABCD中，点E为边AB上的点，BE：AE＝n，连结DE、BD，过点A作AG⊥DE，垂足为点F，与BC、BD分别交于点G、H，连结EH.
(1)、①求证：△ADE≌△BAG；②求证：DH：BH＝n+1；
(2)、如图2，当EH∥AD时，求n的值.22. 如图，直线y＝﹣x+3与x轴、y轴分别交于B、C两点，经过B、C两点的抛物线y＝x2+bx+c与x轴的另一个交点为A，顶点为P.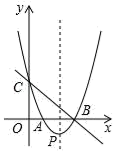
(1)、求该抛物线的解析式；(2)、当0＜x＜3时，在抛物线上求一点E，使△CBE的面积有最大值；(3)、在该抛物线的对称轴上是否存在点M，使以C、P、M为顶点的三角形为等腰三角形？若存在，请写出所符合条件的点M的坐标；若不存在，请说明理由.