贵州省毕节市黔西县2019届九年级上学期期中考试数学试题
试卷更新日期:2019-09-17 类型:期中考试
一、单选题
-
1. 关于x的一元二次方程(a2﹣1)x2+x﹣2=0是一元二次方程,则a满足( )A、a≠1 B、a≠﹣1 C、a≠±1 D、为任意实数2. 下列命题中,正确的是( )A、菱形的对角线相等 B、平行四边形既是轴对称图形,又是中心对称图形 C、正方形的对角线相等且互相垂直 D、矩形的对角线不能相等3. 下列各组线段的长度成比例的是( )A、1cm,2cm,3cm,4cm B、2cm,3cm,4cm,5cm C、0.3m,0.6m,0.5m,0.9m D、30cm,20cm,90cm,60cm4. 已知一元二次方程x2﹣3x﹣3=0的两根为α与β,则 的值为( )A、﹣1 B、1 C、﹣2 D、25. 菱形具有而平行四边形不具有的性质是( )A、两组对边分别平行 B、两组对角分别相等 C、对角线互相平分 D、对角线互相垂直6. 如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
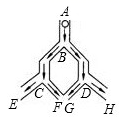 A、 B、 C、 D、7. 一元二次方程x2+px﹣2=0的一个根为2,则p的值为( )A、1 B、2 C、﹣1 D、﹣28. 若m、n是一元二次方程x2-5x-2=0的两个实数根,则m+n-mn的值是( )A、-7 B、7 C、3 D、-39. 已知粉笔盒里有4支红色粉笔和n支白色粉笔,每支粉笔除颜色外均相同,现从中任取一支粉笔,取出红色粉笔的概率是 ,则n的值是( )A、4 B、6 C、8 D、1010. 一元二次方程4x2-x=1的解是( )A、x=0 B、x1=0,x2=4 C、x1=0,x2= D、 ,11. 菱形,矩形,正方形都具有的性质是( )A、对角线相等且互相平分 B、对角线相等且互相垂直平分 C、对角线互相平分 D、四条边相等,四个角相等12. 已知关于x的一元二次方程mx2+2x﹣1=0有两个不相等的实数根,则m的取值范围是( )A、m<﹣1 B、m>1 C、m<1且m≠0 D、m>﹣1且m≠013. 已知关于x的一元二次方程 有一根为0,则k的值是( )A、-1 B、1 C、±1 D、014.
A、 B、 C、 D、7. 一元二次方程x2+px﹣2=0的一个根为2,则p的值为( )A、1 B、2 C、﹣1 D、﹣28. 若m、n是一元二次方程x2-5x-2=0的两个实数根,则m+n-mn的值是( )A、-7 B、7 C、3 D、-39. 已知粉笔盒里有4支红色粉笔和n支白色粉笔,每支粉笔除颜色外均相同,现从中任取一支粉笔,取出红色粉笔的概率是 ,则n的值是( )A、4 B、6 C、8 D、1010. 一元二次方程4x2-x=1的解是( )A、x=0 B、x1=0,x2=4 C、x1=0,x2= D、 ,11. 菱形,矩形,正方形都具有的性质是( )A、对角线相等且互相平分 B、对角线相等且互相垂直平分 C、对角线互相平分 D、四条边相等,四个角相等12. 已知关于x的一元二次方程mx2+2x﹣1=0有两个不相等的实数根,则m的取值范围是( )A、m<﹣1 B、m>1 C、m<1且m≠0 D、m>﹣1且m≠013. 已知关于x的一元二次方程 有一根为0,则k的值是( )A、-1 B、1 C、±1 D、014.如图,菱形ABCD的对角线AC、BD相交于点O,AC=8,BD=6,过点O作OH⊥AB,垂足为H,则点O到边AB的距离OH等于( )
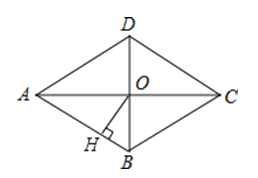 A、2 B、 C、 D、15. 如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
A、2 B、 C、 D、15. 如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )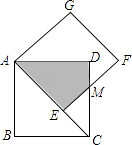 A、﹣4+4 B、4 +4 C、8﹣4 D、 +1
A、﹣4+4 B、4 +4 C、8﹣4 D、 +1二、填空题
-
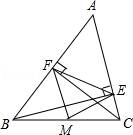
16. 已知 = ,则 .17. 等腰三角形两腰长分别为a,b,且a,b是关于x的一元二次方程x2﹣6x+n﹣1=0的两根,则n的值为.18. 如果甲邀请乙玩一个同时抛掷两枚硬币的游戏。游戏的规则如下:同时抛出两个正面,乙得1分;抛出其他结果,甲得1分。谁先累积得到10分,谁就获胜,你认为(甲或乙)获胜的可能性更大。19. 如图,BE、CF分别是△ABC的高,M为BC的中点,EF=5,BC=8,则△EFM的周长是.
 20. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,P为AB边上(不与A、B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是.
20. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,P为AB边上(不与A、B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是.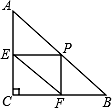
三、解答题
-
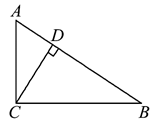
21. 解方程:(1)、2x2+x﹣2=0(用公式法)(2)、(x+3)2﹣2x(x+3)=0.22. 先化简 - ÷ ,再求值.其中a满足方程a2-2a-3=0.23. 如图,已知△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,已知AC=3,BC=4.问线段AD,CD,CD,BD是不是成比例线段?写出你的理由
 24. 如图,在平行四边形ABCD中,点P是对角线AC上的一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?
24. 如图,在平行四边形ABCD中,点P是对角线AC上的一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?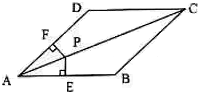 25. 现有三张反面朝上的扑克牌:红桃2、红桃3、黑桃x(1≤x≤13且x为奇数或偶数).把牌洗匀后第一次抽取一张,记好花色和数字后将牌放回,重新洗匀第二次再抽取一张.(1)、求两次抽得相同花色的概率;(2)、当甲选择x为奇数,乙选择x为偶数时,他们两次抽得的数字和是奇数的可能性大小一样吗?请说明理由.(提示:三张扑克牌可以分别简记为红2、红3、黑x)26. 某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售,销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元?27. 在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.
25. 现有三张反面朝上的扑克牌:红桃2、红桃3、黑桃x(1≤x≤13且x为奇数或偶数).把牌洗匀后第一次抽取一张,记好花色和数字后将牌放回,重新洗匀第二次再抽取一张.(1)、求两次抽得相同花色的概率;(2)、当甲选择x为奇数,乙选择x为偶数时,他们两次抽得的数字和是奇数的可能性大小一样吗?请说明理由.(提示:三张扑克牌可以分别简记为红2、红3、黑x)26. 某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售,销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元?27. 在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.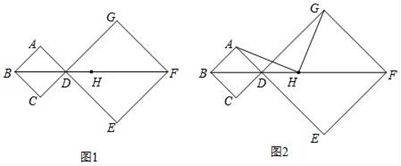 (1)、如图1,若AB=1,DG=2,求BH的长;(2)、如图2,连接AH,GH.
(1)、如图1,若AB=1,DG=2,求BH的长;(2)、如图2,连接AH,GH.小宇观察图2,提出猜想:AH=GH,AH⊥GH.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:延长AH交EF于点M,连接AG,GM,要证明结论成立只需证△GAM是等腰直角三角形;
想法2:连接AC,GE分别交BF于点M,N,要证明结论成立只需证△AMH≌△HNG.…
请你参考上面的想法,帮助小宇证明AH=GH,AH⊥GH.(一种方法即可)