重庆市万州区江南新区联盟2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-09-17 类型:期末考试
一、单选题
-
1. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列说法正确的是( )A、掷一枚硬币,正面一定朝上 B、某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖 C、旅客上飞机前的安检应采用抽样调查 D、方差越大,数据的波动越大3. 如图,一个正六边形转盘被分成6个全等三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是( )
2. 下列说法正确的是( )A、掷一枚硬币,正面一定朝上 B、某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖 C、旅客上飞机前的安检应采用抽样调查 D、方差越大,数据的波动越大3. 如图,一个正六边形转盘被分成6个全等三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是( )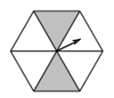 A、 B、 C、 D、4. 将二次函数y=x2的图象向下平移一个单位,则平移以后的二次函数的解析式为( )A、y=x2﹣1 B、y=x2+1 C、y=(x﹣1)2 D、y=(x+1)25. 如图,在⊙O中,弦AC∥半径OB,∠BOC=48°,则∠OAB的度数为( )
A、 B、 C、 D、4. 将二次函数y=x2的图象向下平移一个单位,则平移以后的二次函数的解析式为( )A、y=x2﹣1 B、y=x2+1 C、y=(x﹣1)2 D、y=(x+1)25. 如图,在⊙O中,弦AC∥半径OB,∠BOC=48°,则∠OAB的度数为( ) A、24° B、30° C、50° D、60°6. 菱形ABCD的一条对角线长为6,边AB的长为方程y2﹣7y+10=0的一个根,则菱形ABCD的周长为( )A、8 B、20 C、8或20 D、107. 如图,观察二次函数 的图象,下列结论:① ,② ,③ ,④ .
A、24° B、30° C、50° D、60°6. 菱形ABCD的一条对角线长为6,边AB的长为方程y2﹣7y+10=0的一个根,则菱形ABCD的周长为( )A、8 B、20 C、8或20 D、107. 如图,观察二次函数 的图象,下列结论:① ,② ,③ ,④ .其中正确的是( )
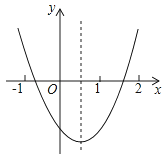 A、①② B、①④ C、②③ D、③④8. 义乌国际小商品博览会某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名两种语言都会翻译.若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是( )A、 B、 C、 D、9. 如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )
A、①② B、①④ C、②③ D、③④8. 义乌国际小商品博览会某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名两种语言都会翻译.若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是( )A、 B、 C、 D、9. 如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( ) A、
A、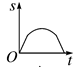 B、
B、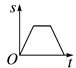 C、
C、 D、
D、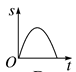 10. 如图(1)是一个水平摆放的小正方体木块,图(2),(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第六个叠放的图形中,小正方体木块总数应是( )
10. 如图(1)是一个水平摆放的小正方体木块,图(2),(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第六个叠放的图形中,小正方体木块总数应是( )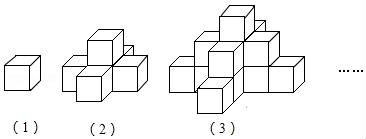 A、25 B、66 C、91 D、12011. 如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3 ;其中正确的结论是( )
A、25 B、66 C、91 D、12011. 如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3 ;其中正确的结论是( )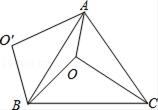 A、①②③ B、①③④ C、②③④ D、①②12. 华润万家超市某服装专柜在销售中发现:进货价为每件50元,销售价为每件90元的某品牌童装平均每天可售出20件.为了迎接“六一”,商场决定采取适当的降价措施,扩大销售量,增加盈利.经调查发现:如果每件童装降价1元,那么平均每天就可多售出2件,要想平均每天销售这种童装盈利1200元,同时又要使顾客得到较多的实惠,设降价x元,根据题意列方程得( )A、(40﹣x)(20+2x)=1200 B、(40﹣x)(20+x)=1200 C、(50﹣x)(20+2x)=1200 D、(90﹣x)(20+2x)=1200
A、①②③ B、①③④ C、②③④ D、①②12. 华润万家超市某服装专柜在销售中发现:进货价为每件50元,销售价为每件90元的某品牌童装平均每天可售出20件.为了迎接“六一”,商场决定采取适当的降价措施,扩大销售量,增加盈利.经调查发现:如果每件童装降价1元,那么平均每天就可多售出2件,要想平均每天销售这种童装盈利1200元,同时又要使顾客得到较多的实惠,设降价x元,根据题意列方程得( )A、(40﹣x)(20+2x)=1200 B、(40﹣x)(20+x)=1200 C、(50﹣x)(20+2x)=1200 D、(90﹣x)(20+2x)=1200二、填空题
-
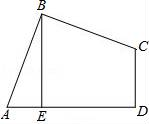
13. 抛物线y=﹣x2+2x﹣3顶点坐标是;对称轴是.14. 一个扇形的半径为3cm,面积为 ,则此扇形的圆心角为.15. 用符号※定义一种新运算:a※b=(a﹣b)×a,则方程x※2=0的解是.16. 若x=﹣1是关于x的一元二次方程ax2+bx﹣2=0(a≠0)的一个根,则代数式2015﹣2a+2b的值为.17. 从﹣1,0,1,2,3这五个数中,随机抽取一个数记为m,则使关于x的不等式组 有解,并且使函数y=(m﹣1)x2+2mx+m+2与x轴有交点的概率为.18. 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为12,则BE的长为.
三、解答题
-
19. 已知:关于x的方程x2+2mx+m2-1=0(1)、不解方程,判别方程根的情况;(2)、若方程有一个根为3,求m的值.20. 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
 (1)、①请画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标;
(1)、①请画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标;②请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(2)、求出(1)②中C点旋转到C2点所经过的路径长(记过保留根号和π).21. 先化简,再求值: ,其中a是方程x2+4x﹣6=0的根.22. 某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:九(1)班.88,91,92,93,93,93,94,98,98,100
九(2)班.89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级
最高分
平均分
中位数
众数
方差
九(1)班
100
m
93
93
12
九(2)班
99
95
n
93
8.4
(1)、直接写出表中m,n的值;(2)、依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;(3)、若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.23. 在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.(1)、求每张门票原定的票价;(2)、根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.24. 已知△ABC是等腰直角三角形,∠A=90°,过点B在∠ABC内作线段BD交AC于点E,过点C作CD⊥BD. (1)、如图1所示,若∠ABD=30°,AB=3,求ED.(2)、如图2所示,若线段BD平分∠ABC,连接AD,求证:AD=CD.(3)、如图3所示,连接AD,求证:BD=CD+ AD.25. 综合与实践:制作无盖盒子
(1)、如图1所示,若∠ABD=30°,AB=3,求ED.(2)、如图2所示,若线段BD平分∠ABC,连接AD,求证:AD=CD.(3)、如图3所示,连接AD,求证:BD=CD+ AD.25. 综合与实践:制作无盖盒子
(1)、任务一:如图1,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折
成高为4cm,容积为616cm3的无盖长方体盒子(纸板厚度忽略不计).

①请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.
②请求出这块矩形纸板的长和宽.
(2)、任务二:图2是一个高为4cm的无盖的五棱柱盒子(直棱柱),图3是其底面,在五边形ABCDE中,BC=12cm,AB=DC=6cm,∠ABC=∠BCD=120°,∠EAB=∠EDC=90°.①试判断图3中AE与DE的数量关系,并加以证明.
②图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果(图中实线表示剪切线,虚线表示折痕.纸板厚度及剪切接缝处损耗忽略不计).
26. 如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).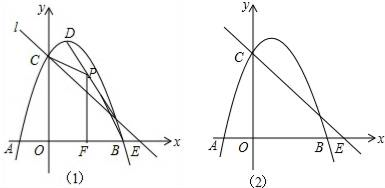 (1)、写出D的坐标和直线l的解析式;(2)、P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;(3)、点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
(1)、写出D的坐标和直线l的解析式;(2)、P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;(3)、点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.