重庆市沙坪坝区2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-09-17 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 在实数-2，-3，0，1中，最小的实数是（   ）
    A、−2 B、−3 C、0 D、1

    查看试题解析

  • 2. 下列图形中是轴对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 3. 计算x3•x2的结果正确的是（   ）
    A、x9 B、x6 C、x5 D、x

    查看试题解析

  • 4. 下列调查中，最合适采用全面调查（普查）方式的是（   ）
    A、对重庆市民知晓“中国梦”内涵情况的调查 B、对2018年元旦节磁器口游客量情况的调查 C、对全国中小学生身高情况的调查 D、对全班同学参加“反邪教”知识问答情况的调查

    查看试题解析

  • 5. 估计2 5 ﹣1的值应在（   ）
    A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

    查看试题解析

  • 6. 若x-2y=-1，则代数式2x-4y+3的值为（   ）
    A、−5 B、0 C、1 D、2

    查看试题解析

  • 7. 要使分式 32−x 有意义，x应满足的条件是（   ）
    A、x>2 B、x<2 C、x=2 D、x≠2

    查看试题解析

  • 8. 若△ABC∽△DEF，相似比为5：4，则对应中线的比为（   ）
    A、5：4 B、5 ：2 C、25：16 D、16：25

    查看试题解析

  • 9. 如图，在△ABC中，AC=BC=4，∠ACB=90°，若点D是AB的中点，分别以点A，B为圆心， 12 AB长为半径画弧，交AC于点E，交BC于点F，则图中阴影部分的面积是（   ）

    A、16−2π B、16−π C、8−2π D、8−π

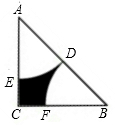    查看试题解析

  • 10. 下列图形都是由同样大小的正方形按照一定规律所组成的，其中第①个图形中一个有2个正方形，第②个图形中一共有8个正方形，第③个图形中一共有16个正方形，…，按此规律，第⑦个图形中正方形的个数为（ ）

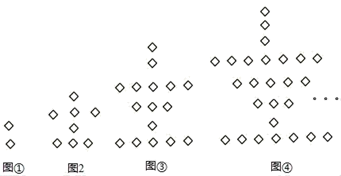    A、56 B、65 C、68 D、71

    查看试题解析

  • 11. 如图，斜坡AB坡度为1：2.4，长度为52米，在坡顶B所在的平台上有一座高楼EF，已知在A处测得楼顶F的仰角为60°，在B处测得楼顶F的仰角为77°，则高楼EF的高度是（   ）（精确到米，参考数据：sin77°≈0.97，tan77°≈4.33， 3 ≈1.73）

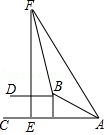    A、125米 B、105米 C、85米 D、65米              

    查看试题解析

  • 12. 如果关于x的分式方程 2+axx−3 -2= 43−x 有正整数解，且关于x的不等式组 {4x<3(x−3)x−a≥0 无解，那么符合条件的所有整数a的和是（   ）
    A、−16 B、−15 C、−6 D、−4

    查看试题解析

二、填空题

  • 13. 据悉，重庆西站2019年将全部建成投入使用，预计客流量每年可达4200万人次，将数4200用科学记数法表示为.

    查看试题解析

  • 14. 计算：|-1|+（ 13 ）-1=.

    查看试题解析

  • 15. 如图，AB，CD是⊙O的弦，且AB⊥CD，连接AD，BC，若∠C=25°，则∠D的度数为.

    查看试题解析

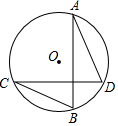  • 16. 为积极响应沙坪坝区创建全国文明城区活动，某校举行了以“弘扬社会主义核心价值观”为主题的征文比赛，校德育处对全校每班的投稿篇数进行了统计，并绘制了如图所示条形统计图，则在本次征文比赛中，平均每班投稿篇数为.

    查看试题解析

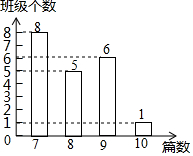  • 17. 老张匀速开车从A市送货到B市，途中汽车出现小故障，老张只能降速为原速的一半行驶等待B市的修车师傅小李前往修车，半小时后，小李与老张相遇，立马开始修车，车修好后，老张又提速为原速的 54 继续开车送货到B市，小李以原速返回B市，老张和小李距离B市的路程y（千米）与老张出发的时间x（小时）的函数图象分别如图所示（途中其它损耗时间忽略不计），则小李在返回到B市时，老张距B市千米.

    查看试题解析

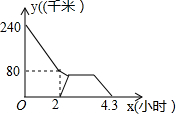  • 18. 如图，在正方形ABCD中，点P是边AB上一点，AB=5BP，点E在对角线AC上，△PEF是直角三角形，PE=PF，AE=2，△APF的面积为12，则BF的长是.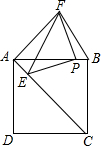

    查看试题解析

三、解答题

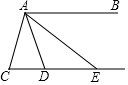
  • 19. 计算：
    (1)、x（x+2y）-（x-y）2；
    (2)、（ 8a+3 +a-3）÷ a2+2a+1a+3 .

    查看试题解析

  • 20. 如图，AB∥CD，∠C=∠ADC，∠BAD的平分线与直线CD相交于点E，若∠CAD=40°，求∠AEC的度数.

    查看试题解析

  • 21. 为学习贯彻党的十九大精神，我区各校积极开展了“党的十九大精神进校园”的宣讲活动，某校为了解学生对党的十九大报告中民生问题的关注情况，随机调查了部分学生，要求被调查的学生只能从A：生态环境、B：医疗卫生、C：文化教育、D：住房保障，四个方面中选择一项，根据调查结果，绘制了如下两幅不完整的统计图：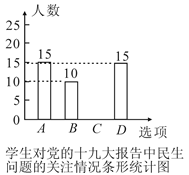

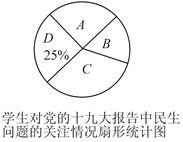
    请解答下列问题：

    (1)、在扇形统计图中B所对应扇形的圆心角等于度，并补全条形统计图；
    (2)、甲乙两位同学对调查的四个方面都非常关注，他们从四个方面随机选择了一个，请用列表或画树状图的方法，求出他们恰好选择到同一个方面的概率.

    查看试题解析

  • 22. 如图，一次函数y=ax+b（a≠0）的图象与反比例函数 y=kx （k≠0）的图象相交于A，B两点，与x轴，y轴分别交于C，D两点，tan∠DCO= 32 ，过点A作AE⊥x轴于点E，若点C是OE的中点，且点A的横坐标为﹣4.，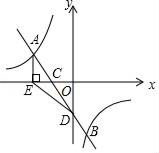

    (1)、求该反比例函数和一次函数的解析式；
    (2)、连接ED，求△ADE的面积.

    查看试题解析

  • 23. 沙坪坝区各街道居民积极响应“创文明城区”活动，据了解，某街道居民人口共有7.5万人，街道划分为A，B两个社区，B社区居民人口数量不超过A社区居民人口数量的2倍.
    (1)、求A社区居民人口至少有多少万人？
    (2)、街道工作人员调查A，B两个社区居民对“社会主义核心价值观”知晓情况发现：A社区有1.2万人知晓，B社区有1.5万人知晓，为了提高知晓率，街道工作人员用了两个月的时间加强宣传，A社区的知晓人数平均月增长率为m%，B社区的知晓人数第一个月增长了 45 m%，第二月在第一个月的基础上又增长了2m%，两个月后，街道居民的知晓率达到92%，求m的值.

    查看试题解析

  • 24. 在等腰Rt△ABC中，∠ACB=90°，AC=BC，点D是边BC上任意一点，连接AD，过点C作CE⊥AD于点E.

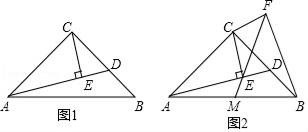    (1)、如图1，若∠BAD=15°，且CE=1，求线段BD的长；
    (2)、如图2，过点C作CF⊥CE，且CF=CE，连接FE并延长交AB于点M，连接BF，求证：AM=BM.

    查看试题解析

  • 25. 一个能被11整除的自然数称为“一心一意数”，它的特征是去掉个位数字后，得到一个新数，新数减去原数的个位数字的差能被11整除，若所得差仍然较大不易判断，则可以再把差去掉个位数字，继续进行下去，直到容易判断为此，如：42581去掉个位是4258，4258减去1的差是4257，4257去掉个位后是425，425减去7的差是418，418去掉个位8后是41，41减去8的差是33，显然33能被11整除，所以42581是“一心一意数”.
    (1)、请用上述规律判断2018和20180116是否是“一心一意数”；
    (2)、一个能被66整除的自然数称为“祥和数”，已知一个四位“祥和数” acbc¯ （千位数字是a，十位数字是b，百位数字和个位数字都是c，0＜a≤9，0≤b≤9，0≤c≤9），求 a+bc 的值.

    查看试题解析

  • 26. 如图，在平面直角坐标系中，抛物线y=x2+2x-3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，对称轴为直线l，点D（-4，n）在抛物线上.

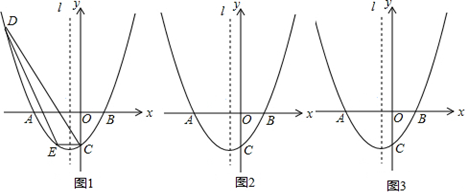    (1)、求直线CD的解析式；
    (2)、E为直线CD下方抛物线上的一点，连接EC，ED，当△ECD的面积最大时，在直线l上取一点M，过M作y轴的垂线，垂足为点N，连接EM，BN，若EM=BN时，求EM+MN+BN的值.
    (3)、将抛物线y=x2+2x-3沿x轴正方向平移得到新抛物线y′，y′经过原点O，y′与x轴的另一个交点为F，设P是抛物线y′上任意一点，点Q在直线l上，△PFQ能否成为以点P为直角顶点的等腰直角三角形？若能，直接写出点P的坐标，若不能，请说明理由.

    查看试题解析