重庆市梁平区2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-09-17 类型:期末考试
一、单选题
-
1. 计算:A、3 B、 C、 D、2. 下列计算正确的是A、 B、 C、 D、3. 在Rt△ABC中,∠C=90°,则 是∠A的( )A、正弦 B、余弦 C、正切 D、以上都不对4. 用配方法法解方程 ,则方程可变形为( )A、 B、 C、 D、5. 已知△ABC∽△A′B′C′,△A′B′C′的面积为6cm2 , 周长为△ABC周长的一半,则△ABC的面积等于( )A、1.5cm2 B、3cm2 C、12cm2 D、24cm26. 某中学开展“眼光体育一小时”活动,根据学校实际情况,如图决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调查,丙将调查结果绘制成如图的统计图,则参加调查的学生中最喜欢跳绳运动项目的学生数为( )
 A、240 B、120 C、80 D、407. 在 和 中,已知 , ,在下面判断中错误的是A、若添加条件 ,则 ≌ B、若添加条件 ,则 ≌ C、若添加条件 ,则 ≌ D、若添加条件 ,则 ≌8. △ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列四个选项中,错误的是( )
A、240 B、120 C、80 D、407. 在 和 中,已知 , ,在下面判断中错误的是A、若添加条件 ,则 ≌ B、若添加条件 ,则 ≌ C、若添加条件 ,则 ≌ D、若添加条件 ,则 ≌8. △ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列四个选项中,错误的是( ) A、sinα=cosα B、tanC=2 C、sinβ=cosβ D、tanα=19. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A、sinα=cosα B、tanC=2 C、sinβ=cosβ D、tanα=19. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )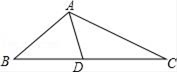 A、4 B、4 C、6 D、410. 若关于x的一元二次方程(k+1)x2+2(k+1)x+k-2=0有实数根,则k的取值范围在数轴上表示正确的是( )A、
A、4 B、4 C、6 D、410. 若关于x的一元二次方程(k+1)x2+2(k+1)x+k-2=0有实数根,则k的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、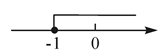 D、
D、 11. 如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
11. 如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84). A、5.1米 B、6.3米 C、7.1米 D、9.2米
A、5.1米 B、6.3米 C、7.1米 D、9.2米二、填空题
-
12. -的相反数是 .13. 方程 的解是.14. 在实数范围内分解因式: .15. 某商品四天内每天每斤的进价与售价的信息如图所示,则售出这种商品每斤利润最大的是第天
 16. 如图,在直角坐标系中,有两点 、 以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为.
16. 如图,在直角坐标系中,有两点 、 以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为.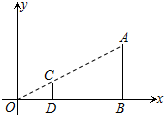 17. 若数a使关于x的不等式组 有且只有四个整数解,且使关于y的方程 的解为非负数,则符合条件的正整数a的值为.
17. 若数a使关于x的不等式组 有且只有四个整数解,且使关于y的方程 的解为非负数,则符合条件的正整数a的值为.三、解答题
-
18. 先化简,再求代数式的值.( + )÷ ,其中a=tan60°﹣sin30°.
19. 九年级一班为推选学生参加“中国古诗词大会的海选活动在班级内举行一次选拔赛成绩分为A,B,C,D四个等级,并将收集到的数据绘制成了如图所示的两幅不完整的统计图请你根据图中所给出的信息解答下列各题. (1)、求九年级一班共有多少人(2)、在扇形统计图中等级为“D”的部分所对应扇形的圆心角为多少度(3)、补全条形统计图和扇形统计图.20. 已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)、求九年级一班共有多少人(2)、在扇形统计图中等级为“D”的部分所对应扇形的圆心角为多少度(3)、补全条形统计图和扇形统计图.20. 已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)、求证:无论m取何值,原方程总有两个不相等的实数根;(2)、若x1 , x2是原方程的两根,且|x1-x2|=2 ,求m的值.
21. 今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75 海里. (1)、求B点到直线CA的距离;(2)、执法船从A到D航行了多少海里?(结果保留根号)22. 如图,在△ABC中,AB=AC=1,BC= ,在AC边上截取AD=BC,连接BD.
(1)、求B点到直线CA的距离;(2)、执法船从A到D航行了多少海里?(结果保留根号)22. 如图,在△ABC中,AB=AC=1,BC= ,在AC边上截取AD=BC,连接BD.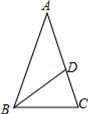 (1)、通过计算,判断AD2与AC•CD的大小关系;(2)、求∠ABD的度数.23. 对任意一个四位数n,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称n为“极数”,记为n= 其中 ,且x、y为整数(1)、请任意写出两个“极数”;(2)、猜想任意一个“极数”是否是99的倍数,请说明理由;(3)、如果一个正整数a是另一个正整数b的平方,则称正整数a是完全平方数,若四位数m为“极数”,记 写出三个满足 是完全平方数的 只需直接写出结果 .24. 某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销.购进价格为每件10元.若售价为12元/件,则可全部售出.若每涨价0.1元.销售量就减少2件.(1)、求该文具店在9月份销售量不低于1100件,则售价应不高于多少元?(2)、由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少 m%.结果10月份利润达到3388元,求m的值(m>10).25. 已知,把 和 按图1摆放, 点C与E点重合 ,点B、C、E、F始终在同一条直线上, , , , , ,如图2, 从图1的位置出发,以每秒1个单位的速度沿CB方向匀速移动,同时,点P从A出发,沿AB以每秒1个单位向点B匀速移动,AC与 的直角边相交于Q,当P到达终点B时, 同时停止运动连接PQ,设移动的时间为 解答下列问题:
(1)、通过计算,判断AD2与AC•CD的大小关系;(2)、求∠ABD的度数.23. 对任意一个四位数n,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称n为“极数”,记为n= 其中 ,且x、y为整数(1)、请任意写出两个“极数”;(2)、猜想任意一个“极数”是否是99的倍数,请说明理由;(3)、如果一个正整数a是另一个正整数b的平方,则称正整数a是完全平方数,若四位数m为“极数”,记 写出三个满足 是完全平方数的 只需直接写出结果 .24. 某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销.购进价格为每件10元.若售价为12元/件,则可全部售出.若每涨价0.1元.销售量就减少2件.(1)、求该文具店在9月份销售量不低于1100件,则售价应不高于多少元?(2)、由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少 m%.结果10月份利润达到3388元,求m的值(m>10).25. 已知,把 和 按图1摆放, 点C与E点重合 ,点B、C、E、F始终在同一条直线上, , , , , ,如图2, 从图1的位置出发,以每秒1个单位的速度沿CB方向匀速移动,同时,点P从A出发,沿AB以每秒1个单位向点B匀速移动,AC与 的直角边相交于Q,当P到达终点B时, 同时停止运动连接PQ,设移动的时间为 解答下列问题: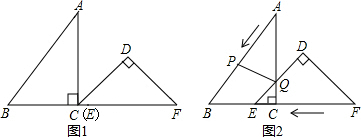 (1)、 在平移的过程中,当点D在 的AC边上时,求AB和t的值;(2)、在移动的过程中,是否存在 为等腰三角形?若存在,求出t的值;若不存在,说明理由.
(1)、 在平移的过程中,当点D在 的AC边上时,求AB和t的值;(2)、在移动的过程中,是否存在 为等腰三角形?若存在,求出t的值;若不存在,说明理由.