重庆市北碚区2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-09-17 类型:期末考试
一、单选题
-
1. 下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、2. 下列式子正确的是( )A、 B、 C、 D、3. 若α、β为方程2x2-5x-1=0的两个实数根,则 的值为( )A、-13 B、12 C、14 D、154. 某钢铁厂一月份生产钢铁560吨,从二月份起,由于改进操作技术,使得第一季度共生产钢铁1850吨,问二、三月份平均每月的增长率是多少?若设二、三月份平均每月的增长率为x,则可得方程( )A、 B、 C、 D、5. 如图所示,每个小正方形的边长均为1,则下列A、B、C、D四个图中的三角形(阴影部分)与△EFG相似的是( )
 A、
A、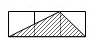 B、
B、 C、
C、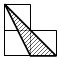 D、
D、 6. 下列说法正确的是( )A、“若ac=bc,则a=b”是必然事件 B、“若|a|+|b|=0,则a=0且b=0”是不确定事件 C、“若ab=0,则a=0且b=0”是不可能事件 D、“若 <0,则a>0且b<0”是随机事件7. 如图,△ABC的面积是12,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是( )
6. 下列说法正确的是( )A、“若ac=bc,则a=b”是必然事件 B、“若|a|+|b|=0,则a=0且b=0”是不确定事件 C、“若ab=0,则a=0且b=0”是不可能事件 D、“若 <0,则a>0且b<0”是随机事件7. 如图,△ABC的面积是12,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是( )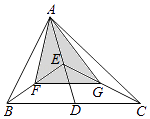 A、4.5 B、5 C、5.5 D、68. 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A、4.5 B、5 C、5.5 D、68. 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )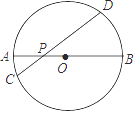 A、 B、2 C、2 D、89. 如图,在 中, ,将 绕顶点C逆时针旋转得到 ,M是 的中点,P是 的中点,连接 .若 ,则线段 的最大值是( )
A、 B、2 C、2 D、89. 如图,在 中, ,将 绕顶点C逆时针旋转得到 ,M是 的中点,P是 的中点,连接 .若 ,则线段 的最大值是( )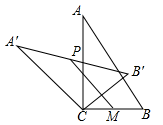 A、4 B、3 C、2 D、110. 已知在△ABC中,∠A,∠B都是锐角, ,则∠C的度数是( )A、30° B、45° C、60° D、90°11. 如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若 =2,则 的值为( )
A、4 B、3 C、2 D、110. 已知在△ABC中,∠A,∠B都是锐角, ,则∠C的度数是( )A、30° B、45° C、60° D、90°11. 如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若 =2,则 的值为( )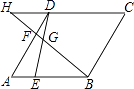 A、 B、 C、 D、12. AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:FC=( )
A、 B、 C、 D、12. AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:FC=( )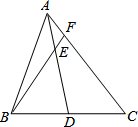 A、1:3 B、1:4 C、1:5 D、1:6
A、1:3 B、1:4 C、1:5 D、1:6二、填空题
-
13. 把 化为最简二次根式,结果是.14. 从-1,0,2,3这四个数中,任取两个数作为a,b,分别代入一元二次方程ax2+bx+2=0中,那么所有可能的一元二次方程中有实数解的一元二次方程的概率为.15. m是方程x2-6x-5=0的一个根,则代数式11+6m-m2的值是.16. 如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是.
 17. 如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= ,反比例函数y= 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于.
17. 如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= ,反比例函数y= 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于.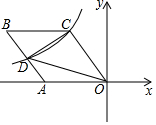 18. 假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过小时车库恰好停满.
18. 假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过小时车库恰好停满.三、解答题
-
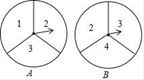
19.(1)、计算:(3 +2 )(3 -2 )-( - )2.(2)、解方程:4(x+3)2-9(x-3)2=0.20. 有两个可以自由转动的均匀转盘A、B都被分成了3等份,并在每一份内均标有数字,如图所示,规则如下:①分别转动转盘A、B;②两个转盘停止后,观察两个指针所指份内的数字(若指针停在等分线上,那么重新转一次,直到指针指向某一份内为止).用列表法(或树状图)求出“两个指针所指的数字都是方程x2﹣3x+2=0的解”的概率.
 21. 已知关于x的一元二次方程 有实数根.(1)、求m的值;(2)、先作 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式.22. 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.
21. 已知关于x的一元二次方程 有实数根.(1)、求m的值;(2)、先作 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式.22. 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.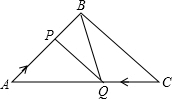 (1)、x为何值时,PQ∥BC;(2)、是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长;若不存在,请说明理由;23. 已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
(1)、x为何值时,PQ∥BC;(2)、是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长;若不存在,请说明理由;23. 已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上. (1)、如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;(2)、如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.24. 2018年兼善中学内的银杏树落叶纷飞,兼善学子决定使用银杏树叶制作精美手工艺品并销售,经市场调研:校徽“善”型手工艺品成本每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:(1)、用表达式表示校徽“善”型手工艺品销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);(2)、兼善学子为了让利给顾客,并同时获得840元利润,售价应定为多少?(3)、当售价定为多少时,兼善学子获得利润最大,最大利润是多少?25. 观察、思考、解答:
(1)、如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;(2)、如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.24. 2018年兼善中学内的银杏树落叶纷飞,兼善学子决定使用银杏树叶制作精美手工艺品并销售,经市场调研:校徽“善”型手工艺品成本每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:(1)、用表达式表示校徽“善”型手工艺品销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);(2)、兼善学子为了让利给顾客,并同时获得840元利润,售价应定为多少?(3)、当售价定为多少时,兼善学子获得利润最大,最大利润是多少?25. 观察、思考、解答:( -1)2=( )2-2×1× +12=2-2 +1=3-2
反之3-2 =2-2 +1=( -1)2
∴3-2 =( -1)2
∴ = -1
(1)、仿上例,化简: ;(2)、若 ,则m、n与a、b的关系是什么?并说明理由;(3)、已知x= ,求( + )• 的值(结果保留根号)26. 有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90o后得到矩形AMEF(如图1),连接BD,MF,若BD=16cm,∠ADB=30o.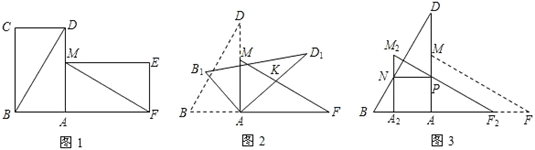 (1)、试探究线段BD 与线段MF的数量关系和位置关系,并说明理由;(2)、把△BCD 与△MEF 剪去,将△ABD绕点A顺时针旋转得△AB1D1 , 边AD1交FM 于点K(如图2),设旋转角为β(0o<β<90o),当△AFK 为等腰三角形时,求β的度数;(3)、若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.
(1)、试探究线段BD 与线段MF的数量关系和位置关系,并说明理由;(2)、把△BCD 与△MEF 剪去,将△ABD绕点A顺时针旋转得△AB1D1 , 边AD1交FM 于点K(如图2),设旋转角为β(0o<β<90o),当△AFK 为等腰三角形时,求β的度数;(3)、若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.