重庆市巴南区2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-09-17 类型:期末考试
一、单选题
-
1. 下列数学符号中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若反比例函数的图象经过点 ,则它的解析式是( )A、 B、 C、 D、3. 下列事件是随机事件的是( )A、太阳东升西落 B、水中捞月 C、明天会下雨 D、人的生命有限4. 已知二次函数 的图象开口向上,则 的取值范围是( )
2. 若反比例函数的图象经过点 ,则它的解析式是( )A、 B、 C、 D、3. 下列事件是随机事件的是( )A、太阳东升西落 B、水中捞月 C、明天会下雨 D、人的生命有限4. 已知二次函数 的图象开口向上,则 的取值范围是( )
A、 B、 C、 D、5. 如图, 是 的直径, 是 的弦,若 ,则 ( )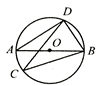 A、 B、 C、 D、6. 如图,将 绕点 按顺时针方向旋转115 后能与 重合,若∠C=90 ,且点 、 、 在同一条直线上,则∠BA 等于( )
A、 B、 C、 D、6. 如图,将 绕点 按顺时针方向旋转115 后能与 重合,若∠C=90 ,且点 、 、 在同一条直线上,则∠BA 等于( )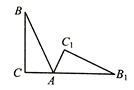 A、 B、 C、 D、7. 已知点 , , 都在反比例函数 的图像上,则( )A、 B、 C、 D、8. 某药品原价为100元,连续两次降价 后,售价为64元,则 的值为( )A、10 B、20 C、23 D、369. 如图,已知 是 的直径,弦 ,垂足为 ,若 , ,则 ( )
A、 B、 C、 D、7. 已知点 , , 都在反比例函数 的图像上,则( )A、 B、 C、 D、8. 某药品原价为100元,连续两次降价 后,售价为64元,则 的值为( )A、10 B、20 C、23 D、369. 如图,已知 是 的直径,弦 ,垂足为 ,若 , ,则 ( )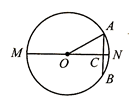 A、 B、 C、 D、210. 已知 是一元二次方程 的一个根,若 ,则下列各数中与 最接近的是( )A、-4 B、-3 C、-2 D、-111. 观察下列一组图形,其中图①中共有5个 ,图②中共有13个 ,图3中共有23个 ,图4中共有35个 ,……,按此规律,图⑧中共有( )
A、 B、 C、 D、210. 已知 是一元二次方程 的一个根,若 ,则下列各数中与 最接近的是( )A、-4 B、-3 C、-2 D、-111. 观察下列一组图形,其中图①中共有5个 ,图②中共有13个 ,图3中共有23个 ,图4中共有35个 ,……,按此规律,图⑧中共有( ) A、103个 B、104个 C、105个 D、106个12. 已知过点 的抛物线 的对称轴是 ,若 ,则( )A、 B、 C、 D、当 时,
A、103个 B、104个 C、105个 D、106个12. 已知过点 的抛物线 的对称轴是 ,若 ,则( )A、 B、 C、 D、当 时,二、填空题
-
13. 一元二次方程 的解是.14. 在数-1,0,1,2中任取两个数作为点的坐标,那么该点刚好在一次函数 图像上的概率是.15. 如图,在 中, , ,点 在边 上,将 绕点 顺时针旋转能与 重合,若 , ,则 的长是.
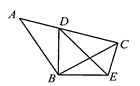 16. 如图,在平行四边形 中, , .以点 为圆心、 为半径画弧交 于点 ,若 ,则图中阴影部分的面积是.
16. 如图,在平行四边形 中, , .以点 为圆心、 为半径画弧交 于点 ,若 ,则图中阴影部分的面积是.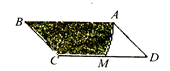 17. 从有理数-3、-2、 、-1、 、0、 、1、 、2、3中,任意取一个数作为 的值,使得关于 的方程 有实数解,且二次函数 与 轴有交点,则满足条件的所有 的值的积是.18. 如图,矩形 的顶点 、 分别在平面直角坐标系的 轴和 轴上,且 ,顶点 在第一象限,经过矩形 对角线交点的反比例函数 的图像分别与 、 交于点 、 ,若 的面积是2,则 的值为.
17. 从有理数-3、-2、 、-1、 、0、 、1、 、2、3中,任意取一个数作为 的值,使得关于 的方程 有实数解,且二次函数 与 轴有交点,则满足条件的所有 的值的积是.18. 如图,矩形 的顶点 、 分别在平面直角坐标系的 轴和 轴上,且 ,顶点 在第一象限,经过矩形 对角线交点的反比例函数 的图像分别与 、 交于点 、 ,若 的面积是2,则 的值为.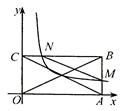
三、解答题
-
19. 解一元二次方程:(1)、 ;(2)、 .20. 如图,已知三点 、 、 . 与 关于 轴对称,点 、 、 分别是点 、 、 的对应点,把 绕点 按顺时针方向旋转 后得到 ,点 、 分别是点 、 的对应点.
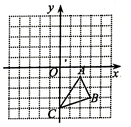 (1)、画出 和 ,并写出点 、 、 的坐标;(2)、旋转过程中,求弧 的长.21. 如图,一次函数 的图像与 轴交于点 ,与反比例函数 的图像交于 ,且 .
(1)、画出 和 ,并写出点 、 、 的坐标;(2)、旋转过程中,求弧 的长.21. 如图,一次函数 的图像与 轴交于点 ,与反比例函数 的图像交于 ,且 . (1)、求 、 、 的值;(2)、直接写出 时 的取值范围.22. 某区某校为了加强对学生的安全教育工作,开展了安全知识竞赛,该校在初三年级中随机抽取了一部分同学的竞赛成绩,并把抽取的竞赛成绩分成优、良、中、差四个等级,同时绘制了如下两幅不完整的统计图,请根据统计图提供的信息解答以下问题:
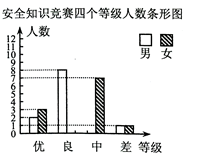
(1)、求 、 、 的值;(2)、直接写出 时 的取值范围.22. 某区某校为了加强对学生的安全教育工作,开展了安全知识竞赛,该校在初三年级中随机抽取了一部分同学的竞赛成绩,并把抽取的竞赛成绩分成优、良、中、差四个等级,同时绘制了如下两幅不完整的统计图,请根据统计图提供的信息解答以下问题: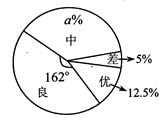
 (1)、该校在初三年级中随机抽取了多少名同学的竞赛成绩?(2)、求扇形统计图中 的值,并补全条形统计图;(3)、若从优等中选出两名同学在全年级进行交流,请用列表或树状图的方法求出所选两名学生恰好是一男一女的概率.23. 某区为了创建国家级卫生城区,对辖区内一些农贸市场需要处理,处理的方式有两种,一种是不改变地理位置就地改造;另一种是改变地理位置,选择一个合理的位置重新建农贸市场.经调研,需要处理的农贸市场共有300万平方米,该区根据区情,限定就地改造的面积不得少于新建面积的2倍.(1)、新建农贸市场的面积最多是多少万平方米?(2)、该区计划以每平方米4000元的造价修建(1)中新建面积最多的农贸市场,以每平方米1000元的造价改造其它需要就地处理的农贸市场.但在实际施工中,新建的农贸市场面积增加了 ,每平方米的造价下降了 ,就地改造的农贸市场的面积没有变,但每平方米的造价下降了 ,结果总费用与计划持平,求 的值.24. 如图1,在 中, , ,将 绕点 旋转,边 分别交边 、 于 、 两点.
(1)、该校在初三年级中随机抽取了多少名同学的竞赛成绩?(2)、求扇形统计图中 的值,并补全条形统计图;(3)、若从优等中选出两名同学在全年级进行交流,请用列表或树状图的方法求出所选两名学生恰好是一男一女的概率.23. 某区为了创建国家级卫生城区,对辖区内一些农贸市场需要处理,处理的方式有两种,一种是不改变地理位置就地改造;另一种是改变地理位置,选择一个合理的位置重新建农贸市场.经调研,需要处理的农贸市场共有300万平方米,该区根据区情,限定就地改造的面积不得少于新建面积的2倍.(1)、新建农贸市场的面积最多是多少万平方米?(2)、该区计划以每平方米4000元的造价修建(1)中新建面积最多的农贸市场,以每平方米1000元的造价改造其它需要就地处理的农贸市场.但在实际施工中,新建的农贸市场面积增加了 ,每平方米的造价下降了 ,就地改造的农贸市场的面积没有变,但每平方米的造价下降了 ,结果总费用与计划持平,求 的值.24. 如图1,在 中, , ,将 绕点 旋转,边 分别交边 、 于 、 两点.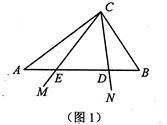
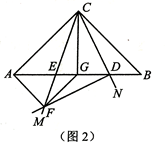 (1)、若 , ,求 的最小值;(2)、如图2,设 ,点 是 的中点,连接 ,当 旋转到 与 的交点 是 的中点时,过点 作 的垂线交CM于点 ,连接 、 ,求证: .25. 已知一个四位自然数M的千、百、十、个位上的数字分别是 、 、 、 ,若 ,且 ,则称自然数M是“关联数”,且规定 .例如5326,因为 ,所以5326是“关联数”,且 现已知式子 ( 、 、 都是整数, , , )的值表示四位自然数 ,且 是“关联数”, 的各位数字之和是8的倍数.(1)、当 时,求 ;(2)、当 时,求 的和.26. 如图,过点 的抛物线 的对称轴是 ,点 是抛物线与 轴的一个交点,点 在 轴上,点 是抛物线的顶点.
(1)、若 , ,求 的最小值;(2)、如图2,设 ,点 是 的中点,连接 ,当 旋转到 与 的交点 是 的中点时,过点 作 的垂线交CM于点 ,连接 、 ,求证: .25. 已知一个四位自然数M的千、百、十、个位上的数字分别是 、 、 、 ,若 ,且 ,则称自然数M是“关联数”,且规定 .例如5326,因为 ,所以5326是“关联数”,且 现已知式子 ( 、 、 都是整数, , , )的值表示四位自然数 ,且 是“关联数”, 的各位数字之和是8的倍数.(1)、当 时,求 ;(2)、当 时,求 的和.26. 如图,过点 的抛物线 的对称轴是 ,点 是抛物线与 轴的一个交点,点 在 轴上,点 是抛物线的顶点.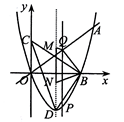
 (1)、求 、 的值;(2)、当 是直角三角形时,求 的面积;(3)、设点 在直线 下方且在抛物线 上,点 、 在抛物线的对称轴上(点 在点 的上方),且 ,过点 作 轴的平行线交直线 于点 ,当 最大时,请直接写出四边形 的周长最小时点 、 、 的坐标.
(1)、求 、 的值;(2)、当 是直角三角形时,求 的面积;(3)、设点 在直线 下方且在抛物线 上,点 、 在抛物线的对称轴上(点 在点 的上方),且 ,过点 作 轴的平行线交直线 于点 ,当 最大时,请直接写出四边形 的周长最小时点 、 、 的坐标.