甘肃省庆阳市镇原县2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-09-17 类型：期中考试
一、单选题
-
1. 下列图形是轴对称图形的有（ ）
A、1个 B、2个 C、3个 D、4个2. 已知△ABC≌△DEF，∠A=80°，∠E=40°，则∠F等于（ ）A、80° B、40° C、60° D、120°3. 小冬不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1，2，3，4的四块），你认为将其中的哪一块带去，能配一块与原来一样大小的三角形？应该带（ ）
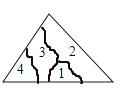A、第1块 B、第2块 C、第3块 D、第4块4. 点P（﹣1，2）关于y轴对称点的坐标是（ ）A、（1，2） B、（﹣1，﹣2） C、（1，﹣2） D、（2，﹣1）5. 等腰三角形一边长是6，另一边长是12，则周长是（ ）A、24 B、30 C、24或30 D、186. 下面各组中的三条线段能组成三角形的是（ ）A、2cm、3cm，5cm B、1cm、6cm、6cm C、2cm、6cm、9cm D、5cm、3cm、10cm7. 一个三角形的两边长分别为3和8，第三边长是一个偶数，则第三边的长不能为（ ）A、6 B、8 C、10 D、128. 过多边形的一个顶点的所有对角线把多边形分成8个三角形，这个多边形的边数是（ ）A、8 B、9 C、10 D、119. 如图，要测量河两岸相对的两点A，B的距离，先在AB的垂线BF上取两点C，D，使CD=BC，再定出BF的垂线DE，使A，C，E在一条直线上，可以证明△EDC≌△ABC，得到ED=AB，因此测得ED的长就是AB的长（如图），判定△EDC≌△ABC的理由是（ ）
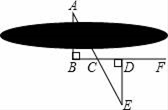A、SAS B、ASA C、SSS D、HL10. 如图：DE是△ABC中AC边的垂直平分线，若BC=8厘米，AB=10厘米，则△EBC的周长为（ ）厘米．
A、16 B、18 C、26 D、2811. 如图，∠A+∠B+∠C+∠D+∠E的度数为（ ）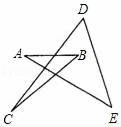
A、90° B、180° C、270° D、360°12. 如图，在△ABE中，∠A=105°，AE的垂直平分线MN交BE于点C，且AB+BC=BE，则∠B的度数是（ ）
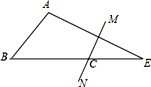A、45° B、60° C、50° D、55°二、填空题
-
13. 一个多边形的各内角都相等，且每个内角与相邻外角的差为100°，那么这个多边形的边数是.14. 已知点P1（5，a﹣1）和点P2（b﹣1，2）关于y轴对称，则（a+b）2017的值为.15. 如图，△ABC中，∠A=70°，点D是BC上一点，BD、CD的垂直平分线分别交AB，AC于点E，F，则∠EDF=度.
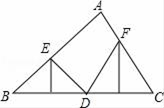16. 一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上，BC与DE交于点M.如果∠ADF=100°，那么∠BMD为度.
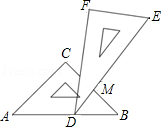17. 如图，CD与BE互相垂直平分，AD⊥DB，∠DBE=70°，则∠ADE=.
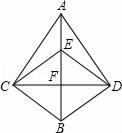18. 如图，已知 是等边三角形，点 是BC上任意一点，OE，OF分别与两边垂直，等边三角形的高为1，则OE+OF的值为.
19. 如图，CE⊥AB，DF⊥AB，垂足分别为E、F，AC∥DB，且AC=BD，那么Rt△AEC≌Rt△BFD的理由是.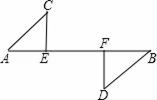
20. 如图所示在△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥BA于E，AB=6厘米，则△DEB的周长是厘米.
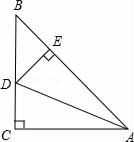21. 如图，AB、CD相交于点O，AD=CB，请你补充一个条件，使得△AOD≌△COB，你补充的条件是.
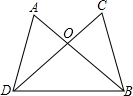22. 在Rt△ABC中，∠ACB=90°，∠CAB=36°，在直线AC或BC上取点M，使得△MAB为等腰三角形，符合条件的M点有个.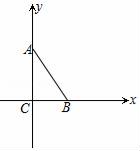
三、解答题
-
23.
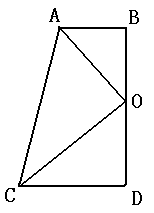
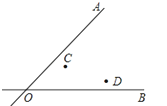
如图，两条公路OA和OB相交于O点，在∠AOB的内部有工厂C和D，现要修建一个货站P，使货站P到两条公路OA、OB的距离相等，且到两工厂C、D的距离相等，用尺规作出货站P的位置．（要求：不写作法，保留作图痕迹，写出结论）
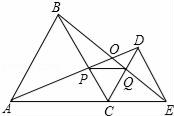
24. 如图，点B，F，C，E在一条直线上，FB=CE，AB∥ED，AC∥FD。求证：AB=DE， AC=DF.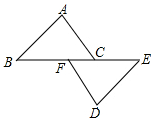
25. 一个多边形的外角和是内角和的 ，求这个多边形的边数和内角和.26. 如图，已知D为△ABC边BC延长线上一点，DF⊥AB于F交AC于E，∠A=35°，∠D=42°，求∠ACD的度数．
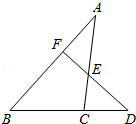27. 如图，∠A=∠B，CE∥DA，CE交AB于E.
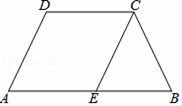(1)、求证：△CEB是等腰三角形；(2)、若AB∥CD，求证：AD=BC.28. 已知：如图，已知△ABC中，其中A（0，﹣2），B（2，﹣4），C（4，﹣1）.
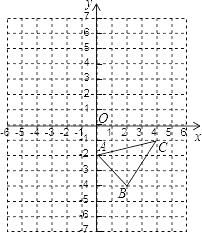(1)、画出与△ABC关于y轴对称的图形△A1B1C1；(2)、写出△A1B1C1各顶点坐标；(3)、求△ABC的面积.
