甘肃省兰州市永登县2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2019-09-17 类型:期中考试
一、单选题
-
1. 下列各数﹣4, ,0, ,π, ,0.101001000…,无理数有( )个.A、1 B、2 C、3 D、42. 若2m-4与3m-1是同一个数的平方根,则m的值是( )A、-3 B、1 C、-3或1 D、-13. 下列各式正确的是( )A、± =3 B、 C、 D、 =±24. 下列函数中,一次函数为( )A、y=x3 B、y=﹣2x+1 C、y= D、y=2x2+15. 若某数的平方等于这个数的本身,则这个数等于( )A、0 B、±1 C、﹣1或0 D、1或06. 平面直角坐标系中,点A(m,﹣2)、B(1,n﹣m)关于x轴对称,则m、n的值为( )A、m=1,n=1 B、m=﹣1,n=1 C、m=1,n=3 D、m=1,n=﹣37. 在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是 和﹣1,则点C所对应的实数是( )
 A、1+ B、2+ C、2 ﹣1 D、2 +18. 一根高9m的旗杆在离地4m高处折断,折断处仍相连,此时在3.9m远处耍的身高为1m的小明( )A、没有危险 B、有危险 C、可能有危险 D、无法判断9. 下列各曲线中表示y是x的函数的是( )A、
A、1+ B、2+ C、2 ﹣1 D、2 +18. 一根高9m的旗杆在离地4m高处折断,折断处仍相连,此时在3.9m远处耍的身高为1m的小明( )A、没有危险 B、有危险 C、可能有危险 D、无法判断9. 下列各曲线中表示y是x的函数的是( )A、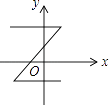 B、
B、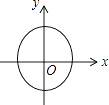 C、
C、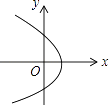 D、
D、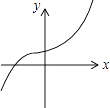 10. 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1, ),则点C的坐标为( )
10. 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1, ),则点C的坐标为( )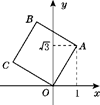 A、(- ,1) B、(-1, ) C、( ,1) D、(- ,-1)11. 一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( )A、
A、(- ,1) B、(-1, ) C、( ,1) D、(- ,-1)11. 一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( )A、 B、
B、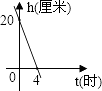 C、
C、 D、
D、 12. 若 的小数部分是a, 的小数部分是b,则a+b的值为( )A、0 B、1 C、-1 D、213. 已知函数 是正比例函数,则m的值是( )A、2 B、﹣2 C、±2 D、14. 正比例函数y=kx(k≠0)函数值y随x的增大而增大,则y=kx﹣k的图象大致是( )A、
12. 若 的小数部分是a, 的小数部分是b,则a+b的值为( )A、0 B、1 C、-1 D、213. 已知函数 是正比例函数,则m的值是( )A、2 B、﹣2 C、±2 D、14. 正比例函数y=kx(k≠0)函数值y随x的增大而增大,则y=kx﹣k的图象大致是( )A、 B、
B、 C、
C、 D、
D、 15. 甲、乙两车从A地出发,沿同一路线驶向B地. 甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时. 由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地. 甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的有( )
15. 甲、乙两车从A地出发,沿同一路线驶向B地. 甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时. 由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地. 甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
16. 的算术平方根是 , 的立方根是 , 绝对值是 .
17. 在 中,斜边AB=2,则 .18. 一棵新栽的树苗高1米,若平均每年都长高5厘米.请写出树苗的高度y(cm)与时间x(年)之间的函数关系式:.19. 在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1 , y1)、P2(x2 , y2)两点,若x1<x2 , 则y1y2 . (填“>”“<”或“=”)20. 如图,已知圆柱体底面圆的半径为 ,高为2,AB、CD分别是两底面的直径,AD、BC是母线,若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短的路线的长度是(结果保留根式)
三、解答题
-
21. 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
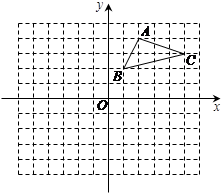
①画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标;②画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2 , 并写出点A2的坐标.
22. 计算:(1)、(2)、 ﹣( +1)2﹣( +1)( ﹣1)(3)、2 ﹣3 +(4)、(2﹣ )0﹣ ﹣ +| ﹣2|23. 已知函数y=(2m+1)x+m+3.(1)、若函数图象经过原点,求m的值;(2)、若函数图象与y轴的交点为(0,﹣2),求m的值;(3)、若函数的图象平行于直线y=3x﹣3,求m的值.24. 已知y﹣3与x成正比例,并且当x=2时,y=7;(1)、求y与x之间的函数关系式;(2)、当x=5时,y的值?25. 如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E. (1)、试判断△BDE的形状,并说明理由;(2)、若AB=4,AD=8,求△BDE的面积.26. 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)、试判断△BDE的形状,并说明理由;(2)、若AB=4,AD=8,求△BDE的面积.26. 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2). (1)、求直线AB的解析式;(2)、若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
(1)、求直线AB的解析式;(2)、若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
