甘肃省定西市陇西县2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2019-09-17 类型:期中考试
一、单选题
-
1. 在以下大众、东风、长城、奔驰四个汽车标志中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下各组线段为边,能组成三角形的是( )A、1cm,2cm,4cm B、8cm,6cm,4cm C、12cm,5cm,6cm D、2cm,3cm,6cm3. 如图,∠1=100°,∠2=145°,那么∠3=( )
2. 以下各组线段为边,能组成三角形的是( )A、1cm,2cm,4cm B、8cm,6cm,4cm C、12cm,5cm,6cm D、2cm,3cm,6cm3. 如图,∠1=100°,∠2=145°,那么∠3=( )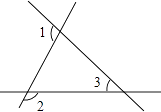 A、55° B、65° C、75° D、85°4. 如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
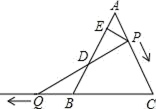
A、55° B、65° C、75° D、85°4. 如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( ) A、SSS B、SAS C、SSA D、ASA5. 已知等腰三角形两边长分别为6cm、2cm,则这个三角形的周长是( )A、14cm B、10cm C、14cm或10cm D、12cm6. 点P是△ABC内一点,连结BP并延长交AC于D,连结PC,则图中∠1、∠2、∠A的大小关系是( )
A、SSS B、SAS C、SSA D、ASA5. 已知等腰三角形两边长分别为6cm、2cm,则这个三角形的周长是( )A、14cm B、10cm C、14cm或10cm D、12cm6. 点P是△ABC内一点,连结BP并延长交AC于D,连结PC,则图中∠1、∠2、∠A的大小关系是( ) A、∠A>∠2>∠1 B、∠1>∠A>∠2 C、∠2>∠1>∠A D、∠1>∠2>∠A7. 如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
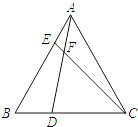
A、∠A>∠2>∠1 B、∠1>∠A>∠2 C、∠2>∠1>∠A D、∠1>∠2>∠A7. 如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )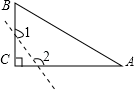 A、90° B、135° C、270° D、315°8. 如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )
A、90° B、135° C、270° D、315°8. 如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )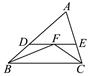 A、③④ B、①② C、①②③ D、②③④9. 如图,点O是△ABC内一点,∠A=80°,∠1=15°,∠2=40°,则∠BOC等于( )
A、③④ B、①② C、①②③ D、②③④9. 如图,点O是△ABC内一点,∠A=80°,∠1=15°,∠2=40°,则∠BOC等于( ) A、95° B、125° C、130° D、135°10. 如图,在 ABC中, A=80 , ABC与 ACD的平分线交于点A1 , 得 A1; A1BC与 A1CD的平分线相交于点A2 , 得 A2;……; A7BC与 A7CD的平分线相交于点A8 , 得 A8 , 则 A8的度数为( )
A、95° B、125° C、130° D、135°10. 如图,在 ABC中, A=80 , ABC与 ACD的平分线交于点A1 , 得 A1; A1BC与 A1CD的平分线相交于点A2 , 得 A2;……; A7BC与 A7CD的平分线相交于点A8 , 得 A8 , 则 A8的度数为( )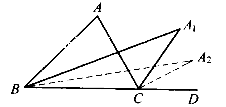 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 三角形的三个内角之比为1∶3∶5,那么这个三角形的最大内角为;12. 一个多边形的每一个外角为30°,那么这个多边形的边数为 .
13. 如图所示,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件 , 使ΔABC≌ΔDBE.(只需添加一个即可) 14. 如图,小明上午在理发店理发时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是.
14. 如图,小明上午在理发店理发时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是. 15. 点A(a,5),B(3,b)关于y轴对称,则a+b=.16. 如图,在△ABC中, ,∠B=30℃D⊥AB于D点,AB=4,则AD的长是.
15. 点A(a,5),B(3,b)关于y轴对称,则a+b=.16. 如图,在△ABC中, ,∠B=30℃D⊥AB于D点,AB=4,则AD的长是.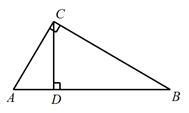 17. 如图,在Rt△ABC中,∠B=90°,AB=3cm,S△ABC=6cm2 , 将△ABC折叠,使点C与点A重合,得折痕DE,则△ABE的周长等于cm.
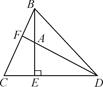
17. 如图,在Rt△ABC中,∠B=90°,AB=3cm,S△ABC=6cm2 , 将△ABC折叠,使点C与点A重合,得折痕DE,则△ABE的周长等于cm. 18. 如图,在 中, , 的垂直平分线交 于点 ,如果 的周长26cm,那么BC= .
18. 如图,在 中, , 的垂直平分线交 于点 ,如果 的周长26cm,那么BC= .
三、解答题
-
19. 有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1 , l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
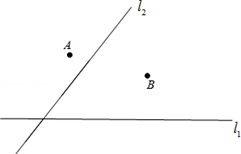 20. 一个多边形的内角和比它外角和的3少180°,求这个多边形的边数.21. 如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:∠A=∠ D.
20. 一个多边形的内角和比它外角和的3少180°,求这个多边形的边数.21. 如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:∠A=∠ D.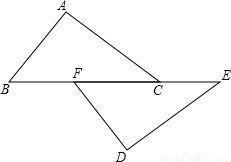 22. 如图,已知D、E两点在线段BC上,AB=AC,AD=AE.证明:BD=CE.
22. 如图,已知D、E两点在线段BC上,AB=AC,AD=AE.证明:BD=CE.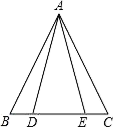 23. 如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,求∠DBC的度数.
23. 如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,求∠DBC的度数.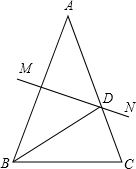 24. △ABC在平面直角坐标系中的位置如图所示.
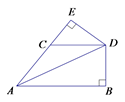
24. △ABC在平面直角坐标系中的位置如图所示. (1)、作出△ABC关于y轴对称的三角形△A1B1C1;将△ABC向下平移3个单位长度,画出平移后的△A2B2C2.(2)、求△A2B2C2.的面积25. 如图,在等腰△ACD中,AC=CD,且CD∥AB,DE⊥AC,交AC延长线于点E,DB⊥AB于B。
(1)、作出△ABC关于y轴对称的三角形△A1B1C1;将△ABC向下平移3个单位长度,画出平移后的△A2B2C2.(2)、求△A2B2C2.的面积25. 如图,在等腰△ACD中,AC=CD,且CD∥AB,DE⊥AC,交AC延长线于点E,DB⊥AB于B。求证:DE=DB.
 26. 已知:BE⊥CD,BE=DE,BC=DA.求证:FD⊥BC.
26. 已知:BE⊥CD,BE=DE,BC=DA.求证:FD⊥BC.