重庆市荣昌区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-09-17 类型:期末考试
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组数据中,能作为一个三角形的三边边长的是( )A、5,5.10 B、5,10,20 C、15,25,35 D、10,15,253. 下列各运算中,计算正确的是( )A、a12÷a3=a4 B、(3a2)3=9a6 C、(a﹣b)2=a2﹣ab+b2 D、2a•3a=6a24. 如图,在正五边形ABCDE中,连接BE,则∠ABE的度数为( )
2. 下列各组数据中,能作为一个三角形的三边边长的是( )A、5,5.10 B、5,10,20 C、15,25,35 D、10,15,253. 下列各运算中,计算正确的是( )A、a12÷a3=a4 B、(3a2)3=9a6 C、(a﹣b)2=a2﹣ab+b2 D、2a•3a=6a24. 如图,在正五边形ABCDE中,连接BE,则∠ABE的度数为( )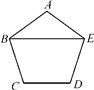 A、30° B、36° C、54° D、72°5. 要使分式 有意义,则x的取值范围是( )A、x≠1 B、x>1 C、x<1 D、x≠﹣16. 小聪将一副直角三角尺如图所示的方式摆放在一起,其中 , , , ,则 ( )
A、30° B、36° C、54° D、72°5. 要使分式 有意义,则x的取值范围是( )A、x≠1 B、x>1 C、x<1 D、x≠﹣16. 小聪将一副直角三角尺如图所示的方式摆放在一起,其中 , , , ,则 ( )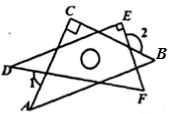 A、180° B、210° C、150° D、240°7. 如图,在 中, . 是 的垂直平分线, 平分 , .则 的长为( )
A、180° B、210° C、150° D、240°7. 如图,在 中, . 是 的垂直平分线, 平分 , .则 的长为( )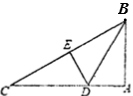 A、6 B、5 C、4 D、38. 若 的值均扩大为原来的2019倍,则下列分式的值保持不变的是( )A、 B、 C、 D、9. “绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是( )A、 B、 C、 D、10. 下列图形都是由相同大小的△按一定规律组成的,其中第(①个图形中一共有3个△,第②个图形中一共有8个△,第③个图形中一共有14个△,…,按此规律排列下去,第⑨个图形中的△个数为( )
A、6 B、5 C、4 D、38. 若 的值均扩大为原来的2019倍,则下列分式的值保持不变的是( )A、 B、 C、 D、9. “绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是( )A、 B、 C、 D、10. 下列图形都是由相同大小的△按一定规律组成的,其中第(①个图形中一共有3个△,第②个图形中一共有8个△,第③个图形中一共有14个△,…,按此规律排列下去,第⑨个图形中的△个数为( ) A、54 B、61 C、71 D、7711. 如图, , ,点 在 边上, , 和 相交于点 ,若 ,则 为( )度.
A、54 B、61 C、71 D、7711. 如图, , ,点 在 边上, , 和 相交于点 ,若 ,则 为( )度. A、 B、 C、 D、12. 若数 使关于 的分式方程 的解为正数,且使关于 的不等式组 的解集为 .则符合条件的所有整数 的和为( )A、8 B、10 C、12 D、16
A、 B、 C、 D、12. 若数 使关于 的分式方程 的解为正数,且使关于 的不等式组 的解集为 .则符合条件的所有整数 的和为( )A、8 B、10 C、12 D、16二、填空题
-
13. 某种细胞的直径为0.000000019米,将数据0.000000019用科学记数法表示为14. 计算: =15. 已知:如图, 是 的边 上的中线, .中线 .则 的取值范围是
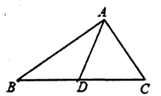 16. 若 是关于x的完全平方式,则m= .17. 如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为.
16. 若 是关于x的完全平方式,则m= .17. 如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为.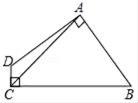 18. 市场上的红茶由茶原液与纯净水按一定比例配制而成,其中购买一吨茶原液的钱可以买15吨纯净水。由于今年以来茶产地连续大旱,茶原液收购价上涨50%.纯净水价也上涨了10%,导致配制的这种茶饮料成本上涨40%,问这种茶饮料中茶原液与纯净水的配制比例为.
18. 市场上的红茶由茶原液与纯净水按一定比例配制而成,其中购买一吨茶原液的钱可以买15吨纯净水。由于今年以来茶产地连续大旱,茶原液收购价上涨50%.纯净水价也上涨了10%,导致配制的这种茶饮料成本上涨40%,问这种茶饮料中茶原液与纯净水的配制比例为.三、解答题
-
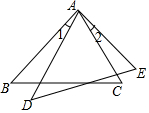
19. 如图,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:BC=DE.
 20. 按要求完成下列各题:(1)、分解因式:(2)、解方程:21. 化简下列各式:(1)、(2)、22. 如图,在 中, , 平分 交 于点 ,过点 作 交 于点 ,且 平分
20. 按要求完成下列各题:(1)、分解因式:(2)、解方程:21. 化简下列各式:(1)、(2)、22. 如图,在 中, , 平分 交 于点 ,过点 作 交 于点 ,且 平分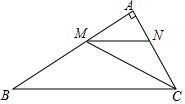 (1)、求 的度数;(2)、若 .求 的长.23. 随着互联网技术的广泛应用,“天猫”、“京东”、“唯品会”等网络大型‘:卖场”的日趋完善,网购成了现代人生活的一部分。与此同时,快递行业也随之高速发展.(1)、如果每名快递员每月最多完成快递投递量相同,且每月投递完l2万件快递量需要快递员比投递完12.6万件快递置需要快递员人数少1人,求每名快递员每月最多完成快递投递量是多少万件;(2)、我市某小型快递公司原有员工20名,随着快递投递任务的加大,该快递公司投入部分资金用于改善投递条件,改善后,每人每月投递快递任务量可增加 ,同时该快递公司又增加了20%的快递员,从而预计每月最大可完成投递快递任务l5.12万件,求 的值.24. 在等腰 中, , ,点 是 上的任意一点,连接 ,过点 作 交 于点 .
(1)、求 的度数;(2)、若 .求 的长.23. 随着互联网技术的广泛应用,“天猫”、“京东”、“唯品会”等网络大型‘:卖场”的日趋完善,网购成了现代人生活的一部分。与此同时,快递行业也随之高速发展.(1)、如果每名快递员每月最多完成快递投递量相同,且每月投递完l2万件快递量需要快递员比投递完12.6万件快递置需要快递员人数少1人,求每名快递员每月最多完成快递投递量是多少万件;(2)、我市某小型快递公司原有员工20名,随着快递投递任务的加大,该快递公司投入部分资金用于改善投递条件,改善后,每人每月投递快递任务量可增加 ,同时该快递公司又增加了20%的快递员,从而预计每月最大可完成投递快递任务l5.12万件,求 的值.24. 在等腰 中, , ,点 是 上的任意一点,连接 ,过点 作 交 于点 .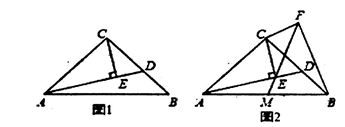 (1)、如图1,若 . , ,求 的面积:(2)、如图2,过 作 ,且 ,连接 并延长 交 于 ,连接 ,求证:25. 若实数 可以表示成两个连续自然数的倒数差,例如, ,所以 是第1个“l阶倒差数”倒差数”, ,所以 是第2个“l阶倒差数”, ,所以 是第3个“l阶倒差数”……,即 ,那么我们称 是第 个“l阶倒差数”;同理, 那么我们称 为第 个“2阶倒差数”。
(1)、如图1,若 . , ,求 的面积:(2)、如图2,过 作 ,且 ,连接 并延长 交 于 ,连接 ,求证:25. 若实数 可以表示成两个连续自然数的倒数差,例如, ,所以 是第1个“l阶倒差数”倒差数”, ,所以 是第2个“l阶倒差数”, ,所以 是第3个“l阶倒差数”……,即 ,那么我们称 是第 个“l阶倒差数”;同理, 那么我们称 为第 个“2阶倒差数”。
(1)、判断 (填是或不是)“1阶倒差数”,第5个“2阶倒差数”是.
(2)、若 均是由两连续奇数组成的“2阶倒差数”,且 .求 的值.26. 已知在四边形 中, , .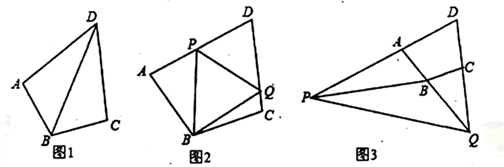 (1)、如图1.连接 ,若 ,求证: .(2)、如图2,点 分别在线段 上,满足 ,求证: ;(3)、若点 在 的延长线上,点 在 的延长线上,如图3所示,仍然满足 ,请写出 与 的数量关系,并给出证明过程.
(1)、如图1.连接 ,若 ,求证: .(2)、如图2,点 分别在线段 上,满足 ,求证: ;(3)、若点 在 的延长线上,点 在 的延长线上,如图3所示,仍然满足 ,请写出 与 的数量关系,并给出证明过程.