重庆市江津区七校2018-2019学年八年级上学期数学期末联考试卷
试卷更新日期：2019-09-17 类型：期末考试
一、单选题
-
1. 下列图形中是轴对称图形的是（ ）A、
B、
C、
D、
2. 若一个三角形的两边长分别是3和4，则第三边的长可能是（ ）A、1 B、2 C、7 D、83. 点（3，﹣2）关于x轴的对称点是（ ）A、（3，2） B、（﹣3，﹣2） C、（﹣3，2） D、（3，﹣2）4. 一个多边形的内角和是1260°，这个多边形的边数是（ ）A、6 B、7 C、8 D、95. 数学活动课上，老师在黑板上画直线平行于射线AN(如图)，让同学们在直线l和射线AN上各找一点B和C ， 使得以A、B、C为顶点的三角形是等腰直角三角形．这样的三角形最多能画( )个．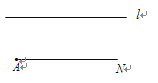
A、1 B、2 C、3 D、46. 将一长方形纸片，按右图的方式折叠，BC，BD为折痕，则∠CBD的度数为（ ）
A、60° B、75° C、90° D、95°7. 若等腰三角形中有一个角等于50°，则这个等腰三角形的顶角的度数为（ ）A、50° B、80° C、65°或50° D、50°或80°8. 下图中显示的是从镜子中看到的背后墙上电子钟的读数，由此你可以推断这时的实际时间是（ ）
A、10：05 B、20：01 C、20：10 D、10：029. 如图，△ABC是等边三角形，BD平分∠ABC，点E在BC的延长线上，且CE=1，∠E=30°，则BC=（ ）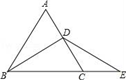
A、1 B、2 C、1.5 D、410. 如图， ABC是等腰三角形，点O 是底边BC上任意一点，OE、OF分别与两边垂直，等腰三角形ABC的腰长为5，面积为12，则OE+OF的值为（ ）
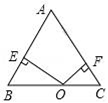A、4 B、 C、15 D、811. 如图，在△ABC中，AB＝AC，∠BAC＝90°，直角∠EPF的顶点P是BC中点，PE、PF分别交AB、AC于点E、F.给出以下四个结论：①AE＝CF；②△EPF是等腰直角三角形；③ 2S四边形AEPF＝S△ABC；④EF＝PC.上述结论正确的有 （ ）.
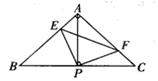A、1个 B、2个 C、3个 D、4个12. 如图，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带（ ）去配.
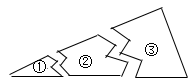A、① B、② C、③ D、①和②二、填空题
-
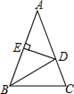
13. 一个多边形的每一个外角都等于36°，则该多边形的内角和等于.14. 如图，△ABC中，AB=AC，∠A=40°，DE是腰AB的垂直平分线，求∠DBC=.
15. 如图所示，已知等边△ABC中，BD＝CE，AD与BE相交于点P，则∠APE是度.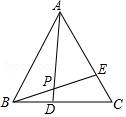
16. 如图，A，B，C，D，E，F是平面上的6个点，则∠A+∠B+∠C+∠D+∠E+∠F=
17. 如图所示，点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P1 ， P2 ， 连接P1P2交OA于M，交OB于N，P1P2＝15，则△PMN的周长为.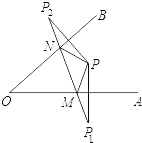
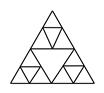
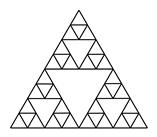
18. 下列图形是将等边三角形按一定规律排列，则第 个图形中所以等边三角形的个数是.
三、解答题
-
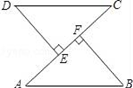
19. 已知：如图，AB=CD，DE⊥AC，BF⊥AC，E，F是垂足AE=CF.求证：DE=BF；
20. 如图，在平面直角坐标系中，△ABC的顶点A（0，1），B（3，2），C（1，4）均在正方形网格的格点上.
(1)、画出△ABC关于x轴对称的图形△A1B1C1；(2)、写出顶点A1 ， B1 ， C1的坐标；(3)、若正方形网格每两个格点间为一个单位长度，求△A1B1C1的面积.21. 如图所示，已知AC∥BD，EA，EB分别平分∠CAB和∠DBA，CD过E点.求证：AB＝AC＋BD.
22. 已知：如图∠BAC的角平分线与BC的垂直平分线DG交于点D，DE⊥AB，DF⊥AC，垂足分别为E，F.
(1)、试说明：BE=CF；(2)、若AF=3，BC=4，求△ABC的周长.23. 阅读下列两则材料：材料一：我们可以将任意三位数记为 （其中a，b，c分别表示该数百位数字、十位数字和个位数字，且a≠0），显然 =100a+10b+c.
材料二：若一个三位数的百位数字、十位数字和个位数字均不为0，则称之为原始数，比如123就是一个原始数，将原始数的三个数位上的数字交换顺序，可产生出5个原始数，比如由123可以产生出132，213，231，312，321这5个原始数.将这6个数相加，得到的和1332称为由原始数123生成的终止数.利用材料解决下列问题：
(1)、分别求出由下列两个原始数生成的终止数：243，537；(2)、若一个原始数 的终止数是另一个原始数 的终止数的3倍，分别求出所有满足条件的这两个原始数.24. 如图，在△ABC中，AB=BC，AD⊥BC于点D，点E为AC中点，连接BE交AD于点F，且BF=AC，过点D作DG∥AB，交AC于点G.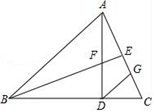
求证：
(1)、∠BAD=2∠DAC
(2)、EF=EG.25. 如图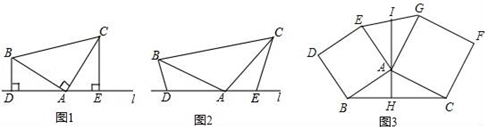
(1)、某学习小组在探究三角形全等时，发现了下面这种典型的基本图形.如图①，已知：在△ABC中，∠BAC=90°，AB=AC，直线L经过点A，BD⊥直线L，CE⊥直线L，垂足分别为点D、E.证明：DE=BD+CE.(2)、组员小刘想，如果三个角不是直角，那结论是否会成立呢？如图②，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线L上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由.(3)、数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图③，过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG，AH是BC边上的高，延长HA交EG于点I，求证：I是EG的中点.