浙江省温州市瑞安市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-09-17 类型:期末考试
一、细心选一选(本题有10小题,每小题3分,共30分)
-
1. 二次根式 在实数范围内有意义,则x应满足的条件是( )A、x≥1 B、x>1 C、x>﹣1 D、x≥﹣12. 若一个多边形的内角和为360°,则这个多边形的边数是( )A、3 B、4 C、5 D、63. 下列选项中,计算正确的是( )A、 + = B、 ÷ =2 C、5 ﹣5 = D、3 -2 =14. 下列各点中,在函数 的图象上的点是( )A、(3,4) B、(﹣2,﹣6) C、(﹣2,6) D、(﹣3,﹣4)5. 小红连续6次掷骰子得到的点数分别是5、4、4、2、1、6.则这组数据的众数是( )A、5 B、4 C、2 D、66. 下列四个手机应用图标中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 7. 下列选项,可以用来证明命题“若a2>b2 , 则a>b”是假命题的反例是( )A、a=3,b=﹣2 B、a=2,b=1 C、a=﹣3,b=2 D、a=﹣2,b=38. 用配方法将方程x2+4x﹣4=0化成(x+m)2=n的形式,则m,n的值是( )A、﹣2,0 B、2,0 C、﹣2,8 D、2,89. 欧几里得是古希腊数学家,所著的《几何原本》闻名于世.在《几何原本》中,形如x2+ax=b2的方程的图解法是:如图,以 和b为直角边作Rt△ABC,再在斜边上截取BD= ,则图中哪条线段的长是方程x2+ax=b2的解?答:是( )
7. 下列选项,可以用来证明命题“若a2>b2 , 则a>b”是假命题的反例是( )A、a=3,b=﹣2 B、a=2,b=1 C、a=﹣3,b=2 D、a=﹣2,b=38. 用配方法将方程x2+4x﹣4=0化成(x+m)2=n的形式,则m,n的值是( )A、﹣2,0 B、2,0 C、﹣2,8 D、2,89. 欧几里得是古希腊数学家,所著的《几何原本》闻名于世.在《几何原本》中,形如x2+ax=b2的方程的图解法是:如图,以 和b为直角边作Rt△ABC,再在斜边上截取BD= ,则图中哪条线段的长是方程x2+ax=b2的解?答:是( ) A、AC B、AD C、AB D、BC10. 如图,将矩形ABCD的四个角向内折叠铺平,恰好拼成一个无缝隙无重叠的矩形EFGH,若EH=5,EF=12,则矩形ABCD的面积是( )
A、AC B、AD C、AB D、BC10. 如图,将矩形ABCD的四个角向内折叠铺平,恰好拼成一个无缝隙无重叠的矩形EFGH,若EH=5,EF=12,则矩形ABCD的面积是( )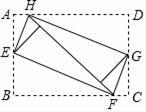 A、13 B、 C、60 D、120
A、13 B、 C、60 D、120二、精心填一填(本题有6小题,每小题3分,共18分)
-
11. 化简: = .12. 写出一个二次项系数为1,解为1与﹣3的一元二次方程: .13. 已知一组数据1,4,a,3,5,若它的平均数是3,则这组数据的中位数是 .14. 如图,矩形ABCD中,对角线AC与BD相交于点O,AB=3,BC=4,则△AOB的周长为 .
 15. 如图,菱形ABCD中,DE⊥AB,垂足为点E,连接CE.若AE=2,∠DCE=30°,则菱形的边长为 .
15. 如图,菱形ABCD中,DE⊥AB,垂足为点E,连接CE.若AE=2,∠DCE=30°,则菱形的边长为 . 16. 如图,反比例函数y= (x>0)的图象经过矩形OABC对角线的交点M,分别交AB、BC于点D、E,连结DE.若四边形ODBE的面积为9,则△ODE的面积是 .
16. 如图,反比例函数y= (x>0)的图象经过矩形OABC对角线的交点M,分别交AB、BC于点D、E,连结DE.若四边形ODBE的面积为9,则△ODE的面积是 .
三、解答题(共4小题,满分27分)
-
17. 解下列方程:(1)、x2﹣3x=0.(2)、(x﹣3)(x﹣1)=8.18. 在▱ABCD中,对角线AC,BD相交于点O,点E,F在AC上且AE=CF,证明:DE=BF.
 19. 如图,图1、图2是两张大小完全相同的6×6方格纸,每个小方格的顶点叫做格点,以格点为顶点的多边形叫做格点多边形.网格中有一个边长为2的格点正方形,按下列要求画出拼图后的格点平行四边形(用阴影表示)
19. 如图,图1、图2是两张大小完全相同的6×6方格纸,每个小方格的顶点叫做格点,以格点为顶点的多边形叫做格点多边形.网格中有一个边长为2的格点正方形,按下列要求画出拼图后的格点平行四边形(用阴影表示)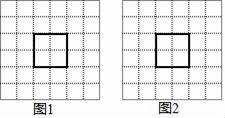 (1)、把图1中的格点正方形分割成两部分,再通过图形变换拼成一个平行四边形,在图1中画出这个格点平行四边形;(2)、把图2中的格点正方形分割成三部分,再通过图形变换拼成一个平行四边形,在图2中画出这个格点平行四边形.20. 某校要从小红、小明和小亮三名同学中挑选一名同学参加数学素养大赛,在最近的四次专题测试中,他们三人的成绩如下表所示:
(1)、把图1中的格点正方形分割成两部分,再通过图形变换拼成一个平行四边形,在图1中画出这个格点平行四边形;(2)、把图2中的格点正方形分割成三部分,再通过图形变换拼成一个平行四边形,在图2中画出这个格点平行四边形.20. 某校要从小红、小明和小亮三名同学中挑选一名同学参加数学素养大赛,在最近的四次专题测试中,他们三人的成绩如下表所示:学生
专题
集合证明
PISA问题
应用题
动点问题
小红
70
75
80
85
小明
80
80
72
76
小亮
75
75
90
65
(1)、请算出小红的平均分为多少?(2)、该校根据四次专题考试成绩的重要程度不同而赋予每个专题成绩一个权重,权重比依次为x:1:2:1,最后得出三人的成绩(加权平均数),若从高分到低分排序为小亮、小明、小红,求正整数x的值.四、耐心做一做(本题有3小题,共25分)
-
21. 某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时,平均每株盈利3元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.(1)、若每盆增加x株,平均每盆盈利y元,写出y关于x的函数表达式;
(2)、要使每盆的盈利为10元,且每盆植入株数尽可能少,问每盆应植入多少株?(3)、若每盆增加x株,平均每盆盈利y元,写出y关于x的函数表达式;
(4)、要使每盆的盈利为10元,且每盆植入株数尽可能少,问每盆应植入多少株?22. 如图,在△ABC中,CA=CB=5,AB=6,AB⊥y轴,垂足为A.反比例函数y= (x>0)的图象经过点C,交AB于点D.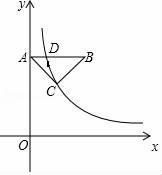 (1)、若OA=8,求k的值;(2)、若CB=BD,求点C的坐标.23. 如图,等腰△ABC中,已知AC=BC=2 , AB=4,作∠ACB的外角平分线CF,点E从点B沿着射线BA以每秒2个单位的速度运动,过点E作BC的平行线交CF于点F.
(1)、若OA=8,求k的值;(2)、若CB=BD,求点C的坐标.23. 如图,等腰△ABC中,已知AC=BC=2 , AB=4,作∠ACB的外角平分线CF,点E从点B沿着射线BA以每秒2个单位的速度运动,过点E作BC的平行线交CF于点F. (1)、求证:四边形BCFE是平行四边形;(2)、当点E是边AB的中点时,连接AF,试判断四边形AECF的形状,并说明理由;(3)、设运动时间为t秒,是否存在t的值,使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形?不存在的,试说明理由;存在的,请直接写出t的值.答:t= .
(1)、求证:四边形BCFE是平行四边形;(2)、当点E是边AB的中点时,连接AF,试判断四边形AECF的形状,并说明理由;(3)、设运动时间为t秒,是否存在t的值,使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形?不存在的,试说明理由;存在的,请直接写出t的值.答:t= .