广西来宾市2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2019-09-17 类型：期末考试

进入出卷网下载

一、选择题：本大题共12小题，每小题3分，共36分.

1. 下列图形中，是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 方程组 ${\begin{matrix} 3 x + 4 y = 5 \\ 2 x - 4 y = 10 \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 3 \\ y = - 1 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = - 1 \end{matrix}$ C、 ${\begin{matrix} x = - 1 \\ y = 2 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$

查看试题解析
3. 下列计算中，正确的是（）

A、2a+3b＝5ab B、（﹣ab）²＝a²b² C、a⁶﹣a⁵＝a D、a•a³＝a³

查看试题解析
4. 下列多项式中能用平方差公式分解因式的是（　　）

A、a²+（﹣b）² B、5m²﹣20mn C、﹣x²﹣y² D、﹣x²+9

查看试题解析
5. 在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：
成绩（m）
1.50
1.60
1.65
1.70
1.75
1.80
人数
1
2
4
3
3
2
这些运动员跳高成绩的中位数和众数分别是（）

A、1.65，1.70 B、1.70，1.70 C、1.70，1.65 D、3，4

查看试题解析
6. 如图，直线a∥b，AC⊥AB，AC交直线b于点C，∠1＝60°，则∠2的度数是（）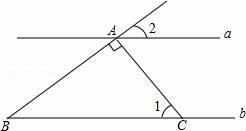

A、50° B、45° C、35° D、30°

查看试题解析
7. 如图是一个旋转对称图形，要使它旋转后与自身重合，至少应将它绕中心逆时针方向旋转的度数为（　　）

A、30° B、60° C、120° D、180°

查看试题解析
8. 下列说法正确的个数有（）
①同位角相等②过一点有且只有一条直线与已知直线垂直③过一点有且只有一条直线与已知直线平行④若a∥b，b∥c，则a∥c．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如果（x﹣2）（x+3）=x²+px+q，那么p、q的值为（　　）

A、p=5，q=6 B、p=1，q=﹣6 C、p=1，q=6 D、p=5，q=﹣6

查看试题解析
10. 如图，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个长方形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（）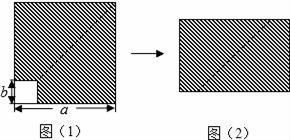

A、（a﹣b）²＝a²﹣2ab+b² B、（a+b）²＝a²+2ab+b² C、a²﹣b²＝（a+b）（a﹣b） D、a²+ab＝a（a+b）

查看试题解析
11. 已知下列算式：①（a³）³＝a⁶； ②a²•a³＝a⁶； ③2^m•3ⁿ＝6^m⁺ⁿ；④﹣a²•（﹣a）³＝a⁵；⑤（a﹣b）³•（b﹣a）²＝（a﹣b）⁵ ．其中计算结果错误的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 定义：直线l₁与l₂相交于点O，对于平面内任意一点M，点M到直线l₁、l₂的距离分别为p、q，则称有序实数对（p，q）是点M的“距离坐标”，根据上述定义，“距离坐标”是（1，2）的点的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题：本大题共6小题，每小题3分，共18分.

13. 若4x²+mx+25是一个完全平方式，则m的值是．

查看试题解析
14. 如图，请添加一个条件，使AB∥CD，那么添加的条件是．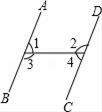

查看试题解析
15. （ $\frac{2}{3}$ ）²⁰²⁰×（﹣1.5）²⁰¹⁹＝．

查看试题解析
16. 若a²﹣b²= $\frac{1}{6}$ ，a﹣b= $\frac{1}{3}$ ，则a+b的值为．

查看试题解析
17. 某体育场的环行跑道长400米，甲、乙同时从同一起点分别以一定的速度练习长跑和骑自行车．如果反向而行，那么他们每隔30秒相遇一次．如果同向而行，那么每隔80秒乙就追上甲一次．甲、乙的速度分别是多少？设甲的速度是x米/秒，乙的速度是y米/秒．则列出的方程组是．

查看试题解析
18. 如图是我国古代数学家杨辉最早发现的，称为“杨辉三角”．它的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！“杨辉三角”中有许多规律，如它的每一行的数字正好对应了（a+b）ⁿ（n为非负整数）的展开式中a按次数从大到小排列的项的系数．例如，（a+b）²＝a²+2ab+b²展开式中的系数1、2、1恰好对应图中第三行的数字；再如，（a+b）³＝a³+3a²b+3ab²+b³展开式中的系数1、3、3、1恰好对应图中第四行的数字．请认真观察此图，写出（a+b）⁴的展开式，（a+b）⁴＝．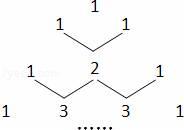

查看试题解析

三、解答题：本大题共8小题，共66分．解答应写出文字说明、证明过程或演算步骤.

19. 如图，在正方形网格上的一个三角形ABC.（其中点A，B，C均在网格上）

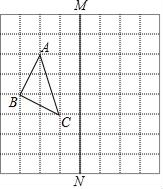
①作出把三角形ABC向右平移4个单位，再向下平移3个单位后所得到的三角形A₁B₁C₁；

②作三角形ABC关于直线MN对称的三角形A₂B₂C₂

查看试题解析
20.

(1)、解方程组： ${\begin{matrix} 2 x + 3 y = 5 \\ 4 x - 3 y = 1 \end{matrix}$

(2)、分解因式：9x²（a﹣b）+y²（b﹣a）．

查看试题解析
21. 先化简，再求值：（a+2b）²+（b+a）（b﹣a），其中a＝﹣1，b＝2．

查看试题解析
22. 如图所示，已知∠ADE＝∠B，FG⊥AB，∠EDC＝∠GFB，求证：CD⊥AB．

查看试题解析

23. 八（2）班组织了一次经典诵读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：

甲	7	8	9	7	10	10	9	10	10	10
乙	10	8	7	9	8	10	10	9	10	9

(1)、甲队成绩的中位数是分，乙队成绩的众数是分；

(2)、计算乙队的平均成绩和方差；

(3)、已知甲队成绩的方差是1.4，则成绩较为整齐的是队．

查看试题解析

24. 如图，直线BC与MN相交于点O，AO⊥BC，OE平分∠BON，若∠EON＝20°，求∠AOM和∠NOC的度数．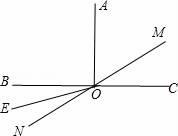

查看试题解析

25. 一方有难八方支援，某市政府筹集了抗旱必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）

车型	甲	乙	丙
汽车运载量（吨/辆）	5	8	10
汽车运费（元/辆）	400	500	600

(1)、若全部物资都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？

(2)、为了节约运费，该市政府可以调用甲、乙、丙三种车型参与运送，已知它们的总辆数为16辆，你能通过列方程组的方法分别求出几种车型的辆数吗？

(3)、求出那种方案的运费最省？最省是多少元．

查看试题解析

26. O为直线AB上的一点，OC⊥OD，射线OE平分∠AOD．

(1)、如图①，判断∠COE和∠BOD之间的数量关系，并说明理由；

(2)、若将∠COD绕点O旋转至图②的位置，试问（1）中∠COE和∠BOD之间的数量关系是否发生变化？并说明理由；

(3)、若将∠COD绕点O旋转至图③的位置，探究∠COE和∠BOD之间的数量关系，并说明理由．

查看试题解析

成绩（m）	1.50	1.60	1.65	1.70	1.75	1.80
人数	1	2	4	3	3	2