广东省珠海市2019-2020学年九年级上学期数学开学考试试卷

试卷更新日期：2019-09-16 类型：开学考试

进入出卷网下载

一、单选题

1. 计算 $\sqrt{8} \times \sqrt{2}$ 的结果是（）

A、 $\sqrt{10}$ B、4 C、8 D、±4

查看试题解析
2. 如图，一棵大树在离地面6米高的B处断裂，树顶A落在离树底部C的8米处，则大树数断裂之前的高度为（）

A、16米 B、15米 C、24米 D、21米

查看试题解析
3. 如图，在矩形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ， $∠ A O B = 60^{°}$ ， $B D = 6$ ，则 $A B$ 的长是（）

A、2 B、3 C、4 D、6

查看试题解析
4. 如图，在菱形 $A B C D$ 中， $A E ， A F$ 分别垂直平分 $B C ， C D$ ，垂足分别为 $E ， F$ ，则 $∠ E A F$ 的度数是（）

A、90° B、60° C、45° D、30°

查看试题解析
5. 矩形各内角的平分线能围成一个（）

A、矩形 B、菱形 C、等腰梯形 D、正方形

查看试题解析
6. 一次函数y=-3x+1的图象一定经过点（）

A、 $(2 ， - 5)$ B、 $(1 ， 0)$ C、 $(- 2 ， 3)$ D、 $(0 ， - 1)$

查看试题解析
7. 若正比例函数y＝kx的图象过点(－2，1)，则一次函数y＝kx－k的图象过（）

A、第一、二、四象限 B、第一、三、四象限 C、第二、三、四象限 D、第一、二、三象限

查看试题解析
8. 用配方法解一元二次方程 $x^{2} - 6 x + 1 = 0$ ，此方程可化为的正确形式是（）

A、 ${(x + 3)}^{2} = 10$ B、 ${(x + 3)}^{2} = 8$ C、 ${(x - 3)}^{2} = 10$ D、 ${(x - 3)}^{2} = 8$

查看试题解析
9. 已知方程 $x^{2} - 5 x + 2 = 0$ 的两个解分别为 $x_{1}$ 、 $x_{2}$ ，则 $x_{1} + x_{2} - x_{1} x_{2}$ 的值为（）

A、 $- 7$ B、 $- 3$ C、7 D、3

查看试题解析
10. 如图，在长为32m ，宽为20m的矩形空地上修建同样宽的道路（图中阴影部分），剩余的空地上种植草坪，使草坪的面积为540m² ．设道路的宽为xm ，根据题意，下面列出的方程正确的是（）

A、32x+20x﹣2x²＝540 B、32x+20x＝32×20﹣540 C、（32﹣x）（20﹣x）＝540 D、（32﹣x）（20﹣x）＝32×20﹣540

查看试题解析

二、填空题

11. 已知两线段的长分别为5cm和3cm，则第三条线段为时，这三条线段构成直角三角形。

查看试题解析
12. 如图，在矩形 $A B C D$ 中， $A D = 8$ ，对角线 $A C$ 与 $B D$ 相交于点 $O$ ， $A E ⊥ B D$ ，垂足为点 $E$ ，且 $A E$ 平分 $∠ B A C$ ，则 $A B$ 的长为.

查看试题解析
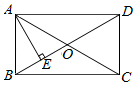13. 如图，正方形ABCD ，以CD为边向正方形内作等边△DEC ，则∠EAB＝º.

查看试题解析
14. 直线y＝kx﹣1与y＝2x平行，则y＝kx﹣1的图象不经过第象限．

查看试题解析
15. 若关于x的一元二次方程 $x^{2} + 2 x + 2 m = 0$ 有两个不相等的实数根，则m的取值范围

查看试题解析
16. 已知m，n是方程x²+2x﹣6=0的一个根，则代数式m²﹣mn+3m+n的值为．

查看试题解析

三、解答题

17.

(1)、用配方法解方程： $x^{2} + 6 x + 4 = 0$ ；

(2)、用公式法解方程： $5 x^{2} - 3 x = x + 1$ .

查看试题解析
18. 如图，四边形ABCD，AB＝AD＝2，BC＝3，CD＝1，∠A＝90°，求∠ADC的度数．

查看试题解析
19. 如图，在 $▱ A B C D$ 中， $A E ⊥ B D$ 于 $E$ ， $C F ⊥ B D$ 于 $F$ ，连接 $A F$ ， $C E$ .求证：四边形 $A E C F$ 是平行四边形.

查看试题解析
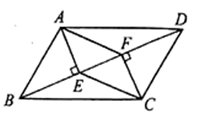20. 如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，-2）．

(1)、求直线AB的解析式；

(2)、若点C在直线AB上，且 $S_{Δ O B C} = 2$ ，求点C的坐标．

查看试题解析
21. 如图，在矩形ABCD中，∠BAD的平分线交BC于点E ，交DC的延长线于点F.

(1)、若AB=2，AD=3，求EF的长；

(2)、若G是EF的中点，连接BG和DG ，
求证：DG=BG.

查看试题解析
22. 如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80m²？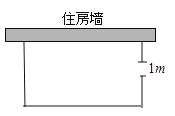

查看试题解析
23. 汽车产业的发展，有效促进我国现代化建设．某汽车销售公司2015年盈利1500万元，到2017年盈利2160万元，且从2015年到2017年，每年盈利的年增长率相同．

(1)、求平均年增长率？

(2)、若该公司盈利的年增长率继续保持不变，预计2018年盈利多少万元？

查看试题解析
24. 已知直线y＝kx+b（k≠0）经过点A（3，0），B（1，2）

(1)、求直线y＝kx+b的函数表达式；

(2)、若直线y＝x﹣2与直线y＝kx+b相交于点C ，求点C的坐标；

(3)、写出不等式kx+b＞x﹣2的解．

查看试题解析
25. 如图，已知四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG。

(1)、求证：矩形DEFG是正方形。

(2)、当点E从A点运动到C点时；
①求证：∠DCG的大小始终不变；

查看试题解析