山东省滨州市阳信县2019-2020学年九年级上学期数学开学考试试卷
试卷更新日期:2019-09-16 类型:开学考试
一、选择题:本大题共12小题,共36分.
-
1. 下列方程是一元二次方程的是( )A、ax2+bx+c=0 B、3x2-2x=3(x2-2) C、x3-2x-4=0 D、(x-1)2+1=02. 三角形两边长分别为3和6,第三边的长是方程x2-13x+36=0的根,则该三角形的周长为( )A、13 B、15 C、18 D、13或183. 已知关于x的一元二次方程(a-1)x2-2x+1=0有两个不相等的实数根,a的取值范围是( )A、a<2 B、a<2且a≠1 C、a>2 D、a<--24. 抛物线y=x2+bx+c的图象向右平移2个单位,再向下平移3个单位,所得图象的解析式为y=x2-2x-3,则b、c的值为( )A、b=2,c=2 B、b=2,c=0 C、b=-2,c=-1 D、b=-3,c=25. 若A( ,y1)、B( ,y2)、C( ,y3)为二次函数y=x2+4x-5的图象上的三个点,则y1、y2、y3的大小关系是( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y1<y3<y26. 已知二次函数y=ax2+bx+c(a≠0)的图象如右图所示,有下列结论:①b2-4ac>0:②abc>0;③8a+c>0;④9a+3b+c<0.其中,正确结论的个数是( )
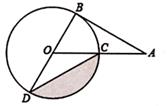
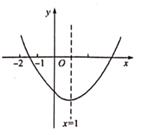 A、1 B、2 C、3 D、47. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、正方形 B、矩形 C、菱形 D、平行四边形8. 已知⊙O的半径为10cm,弦MN∥E,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为( )cm.A、14或2 B、14 C、2 D、69. 如图,AB是⊙O的直径,BC是⊙O的切线,若OC=AB,则∠C的度数为( )
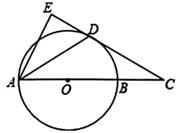
A、1 B、2 C、3 D、47. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、正方形 B、矩形 C、菱形 D、平行四边形8. 已知⊙O的半径为10cm,弦MN∥E,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为( )cm.A、14或2 B、14 C、2 D、69. 如图,AB是⊙O的直径,BC是⊙O的切线,若OC=AB,则∠C的度数为( ) A、15° B、30° C、45° D、60°10. 如图,有一圆内接正八边形 ABCDEFGH,若△ADE的面积为10,则正八边形 ABCDEFGH的面积为( )
A、15° B、30° C、45° D、60°10. 如图,有一圆内接正八边形 ABCDEFGH,若△ADE的面积为10,则正八边形 ABCDEFGH的面积为( )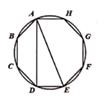 A、40 B、50 C、60 D、8011. 若圆锥的底面半径为2cm,母线长为3cm,则它的侧面积为( )A、2πcm2 B、3πcm2 C、6πcm2 D、12πcm212. 下列说法正确的是( )A、任意掷一枚质地均匀的硬币10次,一定有5次正面向上 B、天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨 C、“篮球队员在罚球线上投篮一次,投中”为随机事件 D、“若a是实数,则|a≥0”是不可能事件
A、40 B、50 C、60 D、8011. 若圆锥的底面半径为2cm,母线长为3cm,则它的侧面积为( )A、2πcm2 B、3πcm2 C、6πcm2 D、12πcm212. 下列说法正确的是( )A、任意掷一枚质地均匀的硬币10次,一定有5次正面向上 B、天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨 C、“篮球队员在罚球线上投篮一次,投中”为随机事件 D、“若a是实数,则|a≥0”是不可能事件二、填空题:本大题共8小题,共40分。
-
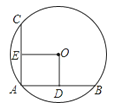
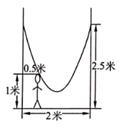
13. 已知方程x2+2x-2=0,则它的两根的倒数和为 .14. 关于x的一元二次方程x2-x-n=0没有实数根,则抛物线y=x2-x-n的顶点在第象限.15. 如右图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为米.
 16. 如图,在Rt△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1 , 则∠A1OB= .
16. 如图,在Rt△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1 , 则∠A1OB= .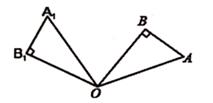 17. 已知⊙O中,弦AB=8cm,圆心到AB的距离为3cm,则此圆的半径为
17. 已知⊙O中,弦AB=8cm,圆心到AB的距离为3cm,则此圆的半径为
18. 如图,AB是⊙0的直径, ∠COD=40°,则∠AOE= .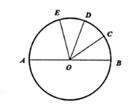 19. 如图,AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD= .
19. 如图,AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD= .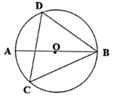 20. 若半径为6cm的圆中,一段弧长为3πcm,则这段弧所对的圆心角度数为 .
20. 若半径为6cm的圆中,一段弧长为3πcm,则这段弧所对的圆心角度数为 .三、解答题:本大题共6个小题,满分74分.
-
21. 若x=-1是关于x的一元二次方程(m-1)x2-x-2=0的一个根,求m的值及另一个根.22. 某茶叶专卖店经销一种日照绿茶,每千克成本80元,据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律。
 (1)、求每月销售量y与销售单价x之间的函数关系式。(2)、若某月该茶叶点销售这种绿茶获得利润1350元,试求该月茶叶的销售单价x为多少元。23. 某商场将进货价30元的书包以40元售出,平均每月能售出600个。市场调查发现:这种书包的售价每上涨1元,其销售量就减少10个。(1)、请写出每月销售书包的利润y(元)与每个书包涨价x(元)之间的函数关系;(2)、设某月的利润为10000元。10000元是否为每月最大利润?如果是,请说明理由;如果不是,请求出最大利润,并求出此时书包的定价应为多少元。(3)、请分析售价在什么范围内商家就可获利。
(1)、求每月销售量y与销售单价x之间的函数关系式。(2)、若某月该茶叶点销售这种绿茶获得利润1350元,试求该月茶叶的销售单价x为多少元。23. 某商场将进货价30元的书包以40元售出,平均每月能售出600个。市场调查发现:这种书包的售价每上涨1元,其销售量就减少10个。(1)、请写出每月销售书包的利润y(元)与每个书包涨价x(元)之间的函数关系;(2)、设某月的利润为10000元。10000元是否为每月最大利润?如果是,请说明理由;如果不是,请求出最大利润,并求出此时书包的定价应为多少元。(3)、请分析售价在什么范围内商家就可获利。