广东省深圳市罗湖区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-09-12 类型:期末考试
一、单选题
-
1. 观察下列图形,其中既是轴对称又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 不等式 的解集在数轴上表示为( )A、
2. 不等式 的解集在数轴上表示为( )A、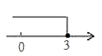 B、
B、 C、
C、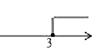 D、
D、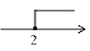 3. 下列从左到右的变形,是分解因式的是( )A、 B、 C、 D、4. 一个多边形的内角和与外角和相等,则这个多边形的边数为( )A、8 B、6 C、5 D、45. 若分式 中 都扩大到原来的3倍,则分式 的值是( )A、扩大到原来3倍 B、缩小3倍 C、是原来的 D、不变6. 如图,在三角形 中, , 平分 交 于点 ,且 , ,则点 到 的距离为( )
3. 下列从左到右的变形,是分解因式的是( )A、 B、 C、 D、4. 一个多边形的内角和与外角和相等,则这个多边形的边数为( )A、8 B、6 C、5 D、45. 若分式 中 都扩大到原来的3倍,则分式 的值是( )A、扩大到原来3倍 B、缩小3倍 C、是原来的 D、不变6. 如图,在三角形 中, , 平分 交 于点 ,且 , ,则点 到 的距离为( )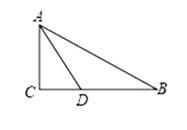 A、 B、 C、 D、7. 如图,将一个含有 角的直角三角板的直角顶点放在一张宽为 的矩形纸带边沿上,另一个顶点在纸带的另一边沿上,若测得三角板的一边与纸带的一边所在的直线成 角,则三角板最长的长是( )
A、 B、 C、 D、7. 如图,将一个含有 角的直角三角板的直角顶点放在一张宽为 的矩形纸带边沿上,另一个顶点在纸带的另一边沿上,若测得三角板的一边与纸带的一边所在的直线成 角,则三角板最长的长是( )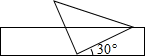 A、 B、 C、 D、8. 如图,在 中, =55°, ,分别以点 和点 为圆心,大于 的长为半径画弧,两弧相交于点 ,作直线 ,交 于点 ,连接 ,则 的度数为( )
A、 B、 C、 D、8. 如图,在 中, =55°, ,分别以点 和点 为圆心,大于 的长为半径画弧,两弧相交于点 ,作直线 ,交 于点 ,连接 ,则 的度数为( )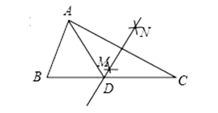 A、 B、 C、 D、9. 下列语句:①每一个外角都等于 的多边形是六边形;②“反证法”就是举反例说明一个命题是假命题;③“等腰三角形两底角相等”的逆命题是真命题;④分式值为零的条件是分子为零且分母不为零,其中正确的个数为( )A、1 B、2 C、3 D、410. 古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为( )
A、 B、 C、 D、9. 下列语句:①每一个外角都等于 的多边形是六边形;②“反证法”就是举反例说明一个命题是假命题;③“等腰三角形两底角相等”的逆命题是真命题;④分式值为零的条件是分子为零且分母不为零,其中正确的个数为( )A、1 B、2 C、3 D、410. 古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为( ) A、 B、 C、 D、11. 如图,等边三角形 的边长为4,点 是△ABC的中心, , 的两边 与 分别相交于 , 绕 点顺时针旋转时,下列四个结论正确的个数是( )
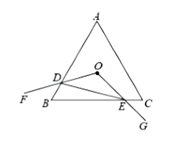
A、 B、 C、 D、11. 如图,等边三角形 的边长为4,点 是△ABC的中心, , 的两边 与 分别相交于 , 绕 点顺时针旋转时,下列四个结论正确的个数是( )① ;② ;③ ;④ 周长最小值是9.
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
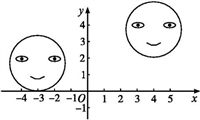
12. 分解因式: .13. 如图所示,在直角坐标系中,右边的图案是由左边的图案经过平移得到的,左边图案中左、右眼睛的坐标分别是(-4,2),(-2,2),右边图案中左眼的坐标是(3,4),则右边图案中右眼的坐标是.
 14. 已知关于 的方程 会产生增根,则 .15. 如图所示,△ABC中,AB=10cm,AC=8cm,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为.
14. 已知关于 的方程 会产生增根,则 .15. 如图所示,△ABC中,AB=10cm,AC=8cm,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为.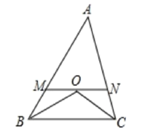
三、解答题
-
16. 解不等式组: 并把其解集在数轴上表示出来.17. 解分式方程:18. 先化简,再求值: ,其中 是不等式 的正整数解.19. 如图,平行四边形 的边 在 轴上,将平行四边形 沿对角线 对折, 的对应线段为 ,且点 在同一直线上, 与 相交于 .
 (1)、求证: ≌ ;(2)、若直线 的函数表达式为 ,求 的面积.20. 某工厂制作甲、乙两种窗户边框,已知同样用12米材料制成甲种边框的个数比制成乙种边框的个数少1个,且制成一个甲种边框比制成一个乙种边框需要多用 的材料.(1)、求制作每个甲种边框、乙种边框各用多少米材料?(2)、如果制作甲、乙两种边框的材料共640米,要求制作乙种边框的数量不少于甲种边框数量的2倍,求应最多安排制作甲种边框多少个(不计材料损耗)?21. 由边长为1的小正方形组成的格点中,建立如图平面直角坐标系,△ABC的三个顶点坐标分别为A(−2,1),B(−4,5),C(−5,2).
(1)、求证: ≌ ;(2)、若直线 的函数表达式为 ,求 的面积.20. 某工厂制作甲、乙两种窗户边框,已知同样用12米材料制成甲种边框的个数比制成乙种边框的个数少1个,且制成一个甲种边框比制成一个乙种边框需要多用 的材料.(1)、求制作每个甲种边框、乙种边框各用多少米材料?(2)、如果制作甲、乙两种边框的材料共640米,要求制作乙种边框的数量不少于甲种边框数量的2倍,求应最多安排制作甲种边框多少个(不计材料损耗)?21. 由边长为1的小正方形组成的格点中,建立如图平面直角坐标系,△ABC的三个顶点坐标分别为A(−2,1),B(−4,5),C(−5,2).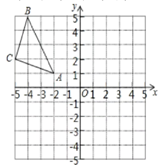 (1)、请画出△ABC关于y轴对称的△A B C ;(2)、画出△ABC关于原点O成中心对称的△A B C ;(3)、请你判断△AA A 与△CC C 的相似比;若不相似,请直接写出△AA A 的面积.22. 如图1,在△ABC中,AB=BC=5,AC=6,△ECD是△ABC沿BC方向平移得到的,连接AE、BE,且AC和BE相交于点O.
(1)、请画出△ABC关于y轴对称的△A B C ;(2)、画出△ABC关于原点O成中心对称的△A B C ;(3)、请你判断△AA A 与△CC C 的相似比;若不相似,请直接写出△AA A 的面积.22. 如图1,在△ABC中,AB=BC=5,AC=6,△ECD是△ABC沿BC方向平移得到的,连接AE、BE,且AC和BE相交于点O.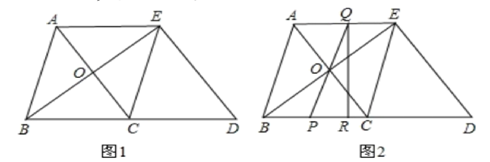 (1)、求证:四边形ABCE是菱形;(2)、如图2,P是线段BC上一动点(不与B.C重合),连接PO并延长交线段AE于点Q,过Q作QR⊥BD交BD于R.
(1)、求证:四边形ABCE是菱形;(2)、如图2,P是线段BC上一动点(不与B.C重合),连接PO并延长交线段AE于点Q,过Q作QR⊥BD交BD于R.①四边形PQED的面积是否为定值?若是,请求出其值;若不是,请说明理由;
②以点P、Q、R为顶点的三角形与以点B.C.O为顶点的三角形是否可能相似?若可能,请求出线段BP的长;若不可能,请说明理由.