广东省深圳市福田区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-09-12 类型:期末考试
一、单选题
-
1. 中, ,则 一定是( )A、锐角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形2. 下列图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若 ,则下列式子中错误的是( )A、 B、 C、 D、4. 因式分解 的正确结果是( )A、 B、 C、 D、5. 要使分式 有意义,则 的取值范围是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、
3. 若 ,则下列式子中错误的是( )A、 B、 C、 D、4. 因式分解 的正确结果是( )A、 B、 C、 D、5. 要使分式 有意义,则 的取值范围是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,一个长为2、宽为1的长方形以下面的“姿态”从直线 的左侧水平平移至右侧(下图中的虚线是水平线),其中,平移的距离是( )
7. 如图,一个长为2、宽为1的长方形以下面的“姿态”从直线 的左侧水平平移至右侧(下图中的虚线是水平线),其中,平移的距离是( ) A、1 B、2 C、3 D、8. 如图,在 中, ,分别以 、 为圆心,以大于 的长为半径画弧,两弧相交于 、 两点,直线 交 于点 ,若 的周长是12,则 的长为( )
A、1 B、2 C、3 D、8. 如图,在 中, ,分别以 、 为圆心,以大于 的长为半径画弧,两弧相交于 、 两点,直线 交 于点 ,若 的周长是12,则 的长为( )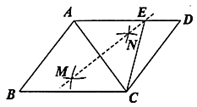 A、6 B、7 C、8 D、119. 如图,直线 的解析式为 ,直线 的解析式为 ,则不等式 的解集是( )
A、6 B、7 C、8 D、119. 如图,直线 的解析式为 ,直线 的解析式为 ,则不等式 的解集是( )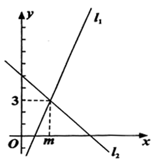 A、 B、 C、 D、10. 如图,将 绕点 按顺时针旋转一定角度得到 ,点 的对应点 恰好落在 边上.若 , ,则 的长为( )
A、 B、 C、 D、10. 如图,将 绕点 按顺时针旋转一定角度得到 ,点 的对应点 恰好落在 边上.若 , ,则 的长为( ) A、1 B、 C、2 D、11. 如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论:①∠AED=∠ADC;② ;③AC BE=12;④3BF=4AC;其中正确结论的个数有( )
A、1 B、 C、2 D、11. 如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论:①∠AED=∠ADC;② ;③AC BE=12;④3BF=4AC;其中正确结论的个数有( )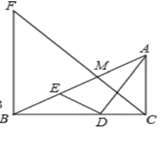 A、1个 B、2个 C、3个 D、4个12. 下列说法正确的是( )A、五边形的内角和是720° B、有两边相等的两个直角三角形全等 C、若关于 的方程 有增根,则 D、若关于 的不等式 恰有2个正整数解,则 的最大值是4
A、1个 B、2个 C、3个 D、4个12. 下列说法正确的是( )A、五边形的内角和是720° B、有两边相等的两个直角三角形全等 C、若关于 的方程 有增根,则 D、若关于 的不等式 恰有2个正整数解,则 的最大值是4二、填空题
-
13. 若 , ,则 的值是.14. 化简 + 的结果为15. 两个实数 , ,规定 ,则不等式 的解集为.16. 如图,已知在 中, ,点 是 延长线上的一点, ,点 是 上一点, ,连接 , 、 分别是 、 的中点,则 .

三、解答题
-
17. 分解因式:(1)、 ;(2)、 .18. 先化简,再求值:
,其中 .
19. 解方程: .20. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(−4,5),(−1,3). (1)、请在如图所示的网格平面内作出平面直角坐标系;(2)、请作出△ABC关于y轴对称的△DEF,其中点A对应点D,点B对应点E,点C对应点F;(3)、写出点E关于原点的对称点M的坐标.21. 如图, 、 是 的对角线 上的两点,且 , ,连接 、 、 、 .
(1)、请在如图所示的网格平面内作出平面直角坐标系;(2)、请作出△ABC关于y轴对称的△DEF,其中点A对应点D,点B对应点E,点C对应点F;(3)、写出点E关于原点的对称点M的坐标.21. 如图, 、 是 的对角线 上的两点,且 , ,连接 、 、 、 . (1)、求证:四边形 为平行四边形;(2)、若 , ,求 的长.22. 王老师从学校出发,到距学校 的某商场去给学生买奖品,他先步行了 后,换骑上了共享单车,到达商场时,全程总共刚好花了 .已知王老师骑共享单车的平均速度是步行速度的3倍(转换出行方式时,所需时间忽略不计).(1)、求王老师步行和骑共享单车的平均速度分别为多少?(2)、买完奖品后,王老师原路返回,为按时上班,路上所花时间最多只剩10分钟,若王老师仍采取先步行,后换骑共享单车的方式返回,问:他最多可步行多少米?23. 如图,在 中, , 是 上的中线, 的垂直平分线 交 于点 ,连接 并延长交 于点 , ,垂足为 .
(1)、求证:四边形 为平行四边形;(2)、若 , ,求 的长.22. 王老师从学校出发,到距学校 的某商场去给学生买奖品,他先步行了 后,换骑上了共享单车,到达商场时,全程总共刚好花了 .已知王老师骑共享单车的平均速度是步行速度的3倍(转换出行方式时,所需时间忽略不计).(1)、求王老师步行和骑共享单车的平均速度分别为多少?(2)、买完奖品后,王老师原路返回,为按时上班,路上所花时间最多只剩10分钟,若王老师仍采取先步行,后换骑共享单车的方式返回,问:他最多可步行多少米?23. 如图,在 中, , 是 上的中线, 的垂直平分线 交 于点 ,连接 并延长交 于点 , ,垂足为 . (1)、求证: ;(2)、若 , ,求 的长;(3)、如图,在 中, , , 是 上的一点,且 ,若 ,请你直接写出 的长.
(1)、求证: ;(2)、若 , ,求 的长;(3)、如图,在 中, , , 是 上的一点,且 ,若 ,请你直接写出 的长.