广东省广州市番禺区2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2019-09-12 类型：期末考试

进入出卷网下载

一、单选题

1. 直线y＝2x﹣6与x轴的交点坐标是（）

A、（0，3） B、（3，0） C、（0，﹣6） D、（﹣3，0）

查看试题解析
2. 下列各式计算正确的是（）

A、 $\sqrt{2^{2}} = \pm 2$ B、 $(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2}) = 3$ C、 $\sqrt{{(- 2)}^{2}} = - 2$ D、 $\sqrt{(- 4) \times (- 9)} = \sqrt{- 4} \times \sqrt{- 9}$

查看试题解析
3. 如图，AC＝AD ， BC＝BD ，则正确的结论是（）

A、AB垂直平分CD B、CD垂直平分AB C、AB与CD互相垂直平分 D、四边形ABCD是菱形

查看试题解析
4. 一组数据5，2，3，5，4，5的众数是（）

A、3 B、4 C、5 D、8

查看试题解析
5. 已知实数a在数轴上的位置如图所示，则化简 $| a | + \sqrt{{(a - 1)}^{2}}$ 的结果为（）

A、1 B、﹣1 C、1﹣2a D、2a﹣1

查看试题解析
6. 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方A、B、C、D的边长分别是3、5、2、3，则最大正方形E的面积是（）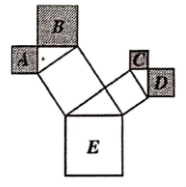

A、13 B、26 C、34 D、47

查看试题解析
7. 下列4个命题：
①对角线相等且互相平分的四边形是正方形；②有三个角是直角的四边形是矩形；③对角线互相垂直的平行四边形是菱形；④一组对边平行，另一组对边相等的四边形是平行四边形其中正确的是（）

A、②③ B、② C、①②④ D、③④

查看试题解析
8. 点P（x ， y）在第一象限，且x+y＝8，点A的坐标为（6，0），设△OPA的面积为S ．当S＝12时，则点P的坐标为（）

A、（6，2） B、（4，4） C、（2，6） D、（12，﹣4）

查看试题解析
9. 如图，直线l₁：y＝x+1与直线l₂：y＝mx+n相交于点P（a ， 2），则关于不等式x+1≥mx+n的解集是（）

A、x≥m B、x≥2 C、x≥1 D、x≥﹣1

查看试题解析
10. 如图，E ， F分别是▱ABCD的边AD、BC上的点，EF＝6，∠DEF＝60°，将四边形EFCD沿EF翻折，得到EFC′D′，ED′交BC于点G ，则△GEF的周长为（）

A、9 B、12 C、9 $\sqrt{3}$ D、18

查看试题解析

二、填空题

11. 计算： $\sqrt{8} \div \sqrt{2}$ ＝．

查看试题解析
12. 如图，在▱ABCD中，若∠A＝63°，则∠D＝．

查看试题解析
13. 将一次函数y＝2x﹣3的图象沿y轴向上平移3个单位长度，所得直线的解析式为．

查看试题解析
14. 如图，等腰三角形中， $A B = A C$ ， $A D$ 是底边上的高 $A B = 5 cm ， B C = 6 cm$ ，则AD=.

查看试题解析
15. 等式 $\sqrt{\frac{a + 1}{3 - a}} = \frac{\sqrt{a + 1}}{\sqrt{3 - a}}$ 成立的条件是．

查看试题解析
16. 如图，正方形A₁B₁C₁O，A₂B₂C₂C₁ ， A₃B₃C₃C₂ ， …按如图所示的方式放置．点A₁ ， A₂ ， A₃ ， …和点C₁ ， C₂ ， C₃ ， …分别在直线 $y = k x + b$ （k＞0）和x轴上，已知点B₁（1，1），B₂（3，2），则B_n的坐标是．

查看试题解析

三、解答题

17. 计算：

(1)、2 $\sqrt{18}$ ﹣ $\sqrt{32}$ + $\sqrt{2}$ ；

(2)、（3+ $\sqrt{2}$ ）×（ $\sqrt{2}$ ﹣5）

查看试题解析
18. 如图，在△ABC中，D、E、F分别为边AB、BC、CA的中点．

(1)、求证：四边形DECF是平行四边形．

(2)、当AC、BC满足何条件时，四边形DECF为菱形？

查看试题解析
19. 如图，在四边形ABCD中，∠D=90°，AB=13，BC=12，CD=4，AD=3.

求：

(1)、AC的长度；

(2)、判断△ACB是什么三角形?并说明理由?

(3)、四边形ABCD的面积。

查看试题解析
20. 甲乙两人参加某项体育训练，近期五次测试成绩得分情况如图所示：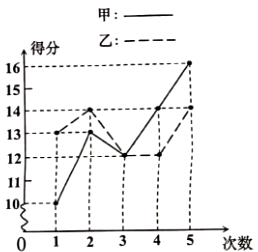

(1)、分别求出两人得分的平均数；

(2)、谁的方差较大？

(3)、根据图表和（1）的计算，请你对甲、乙两人的训练成绩作出评价．

查看试题解析
21. 如图，在四边形ABCD中，AB＝CD ， BF＝DE ， AE⊥BD ， CF⊥BD ，垂足分别为E、F ．

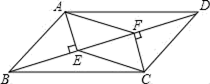(1)、求证：△ABE≌△CDF；

(2)、若AC与BD交于点O ，求证：AO＝CO ．

查看试题解析
22. 如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点．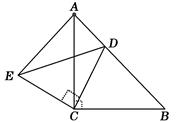

求证：

(1)、△ACE≌△BCD；

(2)、 $A D^{2} + D B^{2} = D E^{2}$ ．

查看试题解析
23. 一次函数y=kx＋b的图象与x、y轴分别交于点A(2，0)，B(0，4)．

(1)、求该函数的解析式；

(2)、O为坐标原点，设OA、AB的中点分别为C、D ， P为OB上一动点，求PC＋PD
的最小值，并求取得最小值时P点的坐标．

查看试题解析
24. 某景点的门票销售分两类：一类为散客门票，价格40元/张，另一类为团体门票（一次性购买门票10张及以上），每张门票价格在散客价格基础上打8折．某班部分同学要去景点旅游，设参加旅游x人，购买门票需要y元．

(1)、如果每人分别买票，求y与x之间的函数解析式．

(2)、如果买团体票，求y与x之间的函数解析式，并写出自变量的取值范围．

(3)、请根据人数变化设计一种比较省钱的购票方案．

查看试题解析
25. 在▱ABCD中，∠ADC的平分线交直线BC于点E ，交直线AB于点F ．

(1)、如图①，证明：BE＝BF ．

(2)、如图②，若∠ADC＝90°，O为AC的中点，G为EF的中点，试探究OG与AC的位置关系，并说明理由．

(3)、如图③，若∠ADC＝60°，过点E作DC的平行线，并在其上取一点K（与点F位于直线BC的同侧），使EK＝BF ，连接CK ， H为CK的中点，试探究线段OH与HA之间的数量关系，并对结论给予证明．

查看试题解析