广东省佛山市顺德区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-09-12 类型:期末考试
一、单选题
-
1. 不等式 的解集在数轴上表示为( )A、
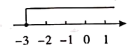 B、
B、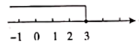 C、
C、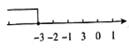 D、
D、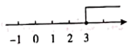 2. 下列图形是中心对称图形,但不是轴对称图形的是( )A、
2. 下列图形是中心对称图形,但不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 若 ,则变形正确的是( )A、 B、 C、 D、4. 一个多边形的内角和是 ,这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形5. 如图是一次函数 ( 、 是常数)的图象,则不等式 的解集是( )
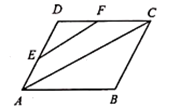
3. 若 ,则变形正确的是( )A、 B、 C、 D、4. 一个多边形的内角和是 ,这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形5. 如图是一次函数 ( 、 是常数)的图象,则不等式 的解集是( ) A、 B、 C、 D、6. 分式运算正确的是( )A、 B、 C、 D、7. 等腰三角形的两条边长分别为3和4,则其周长等于( )A、10 B、11 C、10或11 D、不确定8. 下列命题是假命题的是( )A、两直线平行,同位角相等 B、两组对角分别相等的四边形是平行四边形 C、若 ,则 D、若 ,则9. 已知 、 、 是 的三边,且满足 ,则 的形状是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、不能确定10. 如图, 、 分别是平行四边形 的边 、 上的点,且 , 分别交 、 于点 、 .下列结论:①四边形 是平行四边形;② ;③ ;④ ,其中正确的个数是( )
A、 B、 C、 D、6. 分式运算正确的是( )A、 B、 C、 D、7. 等腰三角形的两条边长分别为3和4,则其周长等于( )A、10 B、11 C、10或11 D、不确定8. 下列命题是假命题的是( )A、两直线平行,同位角相等 B、两组对角分别相等的四边形是平行四边形 C、若 ,则 D、若 ,则9. 已知 、 、 是 的三边,且满足 ,则 的形状是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、不能确定10. 如图, 、 分别是平行四边形 的边 、 上的点,且 , 分别交 、 于点 、 .下列结论:①四边形 是平行四边形;② ;③ ;④ ,其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 因式分解:x2+6x= .12. 分式 有意义时 的取值范围是.13. 若 是完全平方式,则 的值是.14. 如图,点 、 分别是平行四边形 的两边 、 的中点.若 的周长是30,则 的周长是.
 15. 如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交边AC于点D,且∠DBC=15°,则∠A的度数是.
15. 如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交边AC于点D,且∠DBC=15°,则∠A的度数是. 16. 已知不等式组 的解集为 ,则 的值是.
16. 已知不等式组 的解集为 ,则 的值是.三、解答题
-
17. 解不等式组18. 先化简,再求值: ,其中 .19. 城市到 城市的铁路里程是300千米.若旅客从 城市到 城市可选择高铁和动车两种交通工具,高铁速度是动车速度的1.5倍,时间相差0.5小时,求高铁的速度.20. 如图, 中, .
 (1)、用尺规作图法在 上找一点 ,使得点 到边 、 的距离相等(保留作图痕迹,不用写作法;(2)、在(1)的条件下,若 , ,求 的长.21. 如图,在平行四边形 中, ,点 为 的中点,连接 并延长与 的延长线相交于点 ,连接 .
(1)、用尺规作图法在 上找一点 ,使得点 到边 、 的距离相等(保留作图痕迹,不用写作法;(2)、在(1)的条件下,若 , ,求 的长.21. 如图,在平行四边形 中, ,点 为 的中点,连接 并延长与 的延长线相交于点 ,连接 . (1)、求证: ;(2)、求证: 是 的平分线.22. 如图,点 为平面直角坐标系的原点,点 在 轴的正半轴上,正方形 的边长是3,点 在 上,且 .将 绕着点 逆时针旋转得到 .
(1)、求证: ;(2)、求证: 是 的平分线.22. 如图,点 为平面直角坐标系的原点,点 在 轴的正半轴上,正方形 的边长是3,点 在 上,且 .将 绕着点 逆时针旋转得到 . (1)、求证: ;(2)、在x轴上找一点 ,使得 的值最小,求出点 的坐标.23. 已知一次函数 , .(1)、若方程 的解是正数,求 的取值范围;(2)、若以 、 为坐标的点 在已知的两个一次函数图象上,求 的值;(3)、若 ,求 的值.
(1)、求证: ;(2)、在x轴上找一点 ,使得 的值最小,求出点 的坐标.23. 已知一次函数 , .(1)、若方程 的解是正数,求 的取值范围;(2)、若以 、 为坐标的点 在已知的两个一次函数图象上,求 的值;(3)、若 ,求 的值.


