广东省东莞市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-09-12 类型:期末考试
一、单选题
-
1. 使代数式 有意义的x的取值范围是( )A、 B、 C、 D、2. 化简 的结果是( )A、 B、 C、 D、3. 某快递公司快递员张海六月第三周投放快递物品件数为:有1天是41件,有2天是35件,有4天是37件,这周里张海日平均投递物品件数为( )A、36件 B、37件 C、38件 D、38.5件4. 甲、乙、丙、丁四位选手各射击10次,每人的平均成绩都是9.3环,方差如表:
选手
甲
乙
丙
丁
方差(环2)
0.035
0.016
0.022
0.025
则这四个人中成绩发挥最稳定的是( )
A、甲 B、乙 C、丙 D、丁5. 已知三条线段长a、b、c满足a2=c2﹣b2 , 则这三条线段首尾顺次相接组成的三角形的形状是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形6. 若一个直角三角形的两边长为12、13,则第三边长为( )A、5 B、17 C、5或17 D、5或7. 如图,在▱ABCD中,下列结论不一定正确的是( )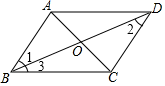 A、∠1=∠2 B、∠1=∠3 C、AB=CD D、∠BAD=∠BCD8. 在四边形ABCD中,AC=BD.顺次连接四边形ABCD四边中点E、F、G、H,则四边形EFGH的形状是( )A、矩形 B、菱形 C、正方形 D、不能确定9. 一个正比例函数的图象经过(1,﹣3),则它的表达式为( )A、y=﹣3x B、y=3x C、y= D、y=﹣10. 某蓄水池的横断面示意图如图所示,分深水区和浅水区,如果以固定的流量把水蓄满蓄水池,下面的图象能大致表示水的深度h和注水时间t之间关系的是( )
A、∠1=∠2 B、∠1=∠3 C、AB=CD D、∠BAD=∠BCD8. 在四边形ABCD中,AC=BD.顺次连接四边形ABCD四边中点E、F、G、H,则四边形EFGH的形状是( )A、矩形 B、菱形 C、正方形 D、不能确定9. 一个正比例函数的图象经过(1,﹣3),则它的表达式为( )A、y=﹣3x B、y=3x C、y= D、y=﹣10. 某蓄水池的横断面示意图如图所示,分深水区和浅水区,如果以固定的流量把水蓄满蓄水池,下面的图象能大致表示水的深度h和注水时间t之间关系的是( )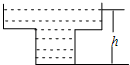 A、
A、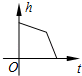 B、
B、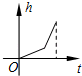 C、
C、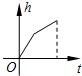 D、
D、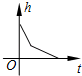
二、填空题
-
11. 计算: = .12. 数据15、19、15、18、21的中位数为 .13. 一次函数y=mx﹣4中,若y随x的增大而减小,则m的取值范围是14. 在Rt△ABC中,∠C=90°,∠A=30°,BC=6,那么AB= .
 15. 如图,将一张矩形纸片ABCD沿EF折叠,使点D与点B重合,点C落在C'的位置上,若∠BFE=67°,则∠ABE的度数为 .
15. 如图,将一张矩形纸片ABCD沿EF折叠,使点D与点B重合,点C落在C'的位置上,若∠BFE=67°,则∠ABE的度数为 .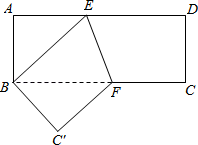
三、解答题
-
16. 计算: +( ﹣1)2﹣17. 一组数据:1,3,2,5,x的平均数是3.(1)、求x的值;(2)、求这组数据的方差.18. 如图,E、F分别为▱ABCD的边BC、AD上的点,且∠1=∠2.求证:四边形AECF是平行四边形.
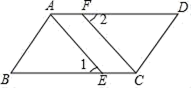 19. 如图,已知在△ABC中,AB=AC=13cm,D是AB上一点,且CD=12cm,BD=8cm.
19. 如图,已知在△ABC中,AB=AC=13cm,D是AB上一点,且CD=12cm,BD=8cm. (1)、求证:△ADC是直角三角形;(2)、求BC的长20. 某水果批发市场规定,批发苹果不少于100千克时,批发价为每千克3.5元,小王携带现金7000元到这市场购苹果,并以批发价买进.如果购买的苹果为x千克,小王付款后的剩余现金为y元(1)、写出y关于x的函数关系式,并写出自变量x的取值范围;(2)、若小王购买800千克苹果,则小王付款后剩余的现金为多少元?21. 已知x=2﹣ ,y=2+ ,求下列代数式的值(1)、x2+2xy+y2;(2)、22. A,B两店分另选5名销售员某月的销售额(单位:万元)进行分析,
(1)、求证:△ADC是直角三角形;(2)、求BC的长20. 某水果批发市场规定,批发苹果不少于100千克时,批发价为每千克3.5元,小王携带现金7000元到这市场购苹果,并以批发价买进.如果购买的苹果为x千克,小王付款后的剩余现金为y元(1)、写出y关于x的函数关系式,并写出自变量x的取值范围;(2)、若小王购买800千克苹果,则小王付款后剩余的现金为多少元?21. 已知x=2﹣ ,y=2+ ,求下列代数式的值(1)、x2+2xy+y2;(2)、22. A,B两店分另选5名销售员某月的销售额(单位:万元)进行分析,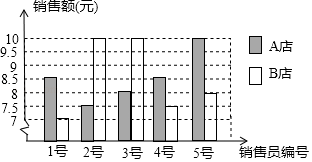 (1)、数据如下图表(不完整):
(1)、数据如下图表(不完整):平均数
中位数
众数
A店
8.5
B店
8
10
根据图a数据填充表格b所缺的数据;
(2)、如果A店想让一半以上的销售员达到销售目标,你认为月销售额定为多少合适?说明理由.23. 如图,在四边形ABCD中,AD∥BC,CA平分∠DCB,DB平分∠ADC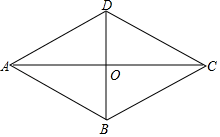 (1)、求证:四边形ABCD是菱形;(2)、若AC=8,BD=6,求点D到AB的距离24. 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(﹣3,0),与y轴交点为B,且与正比例函数y= x的图象交于点C(m,4)
(1)、求证:四边形ABCD是菱形;(2)、若AC=8,BD=6,求点D到AB的距离24. 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(﹣3,0),与y轴交点为B,且与正比例函数y= x的图象交于点C(m,4)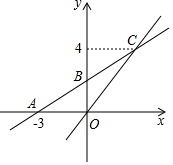 (1)、求m的值及一次函数y=kx+b的表达式;(2)、观察函数图象,直接写出关于x的不等式 x≤kx+b的解集;(3)、若P是y轴上一点,且△PBC的面积是8,直接写出点P的坐标.25. 如图,已知正方形ABCD的边长是2,点E是AB边上一动点(点E与点A、B不重合),过点E作FG⊥DE交BC边于点F、交DA的延长线于点G,且FH∥AB.
(1)、求m的值及一次函数y=kx+b的表达式;(2)、观察函数图象,直接写出关于x的不等式 x≤kx+b的解集;(3)、若P是y轴上一点,且△PBC的面积是8,直接写出点P的坐标.25. 如图,已知正方形ABCD的边长是2,点E是AB边上一动点(点E与点A、B不重合),过点E作FG⊥DE交BC边于点F、交DA的延长线于点G,且FH∥AB.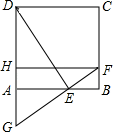 (1)、当DE= 时,求AE的长;(2)、求证:DE=GF;(3)、连结DF,设AE=x,△DFG的面积为y,求y与x之间的函数关系式.
(1)、当DE= 时,求AE的长;(2)、求证:DE=GF;(3)、连结DF,设AE=x,△DFG的面积为y,求y与x之间的函数关系式.