广东省江门市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-09-12 类型:期末考试
一、单选题
-
1. 下列各式是最简二次根式的是( )A、 B、 C、 D、2. 以下列各数为边长,能构成直角三角形的是( )A、1, ,2 B、 , , C、5,11,12 D、9,15,173. 下列函数中,正比例函数是( )A、y= B、y=− C、y=x+4 D、y=x24. 某校九年级“诗歌大会”比赛中,各班代表队得分如下(单位:分):9,7,8,7,9,7,6,则各代表队得分的中位数是( )A、9分 B、8分 C、7分 D、6分5. D,E是△ABC的边AB、AC的中点,△ABC、△ADE的面积分别为S、S1 , 则下列结论中,错误的是( )A、DE∥BC B、DE= BC C、S1= S D、S1= S6. 四边形ABCD中,AB∥CD,要使ABCD是平行四边形,需要补充的一个条件( )A、AD=BC B、AB=CD C、∠DAB=∠ABC D、∠ABC=∠BCD7. 如图,四边形ABCD是菱形,DH⊥AB于点H,若AC=8cm,BD=6cm,则DH=( )
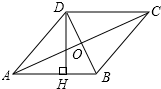 A、5 cm B、 cm C、 cm D、 cm8. 已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的表达式为( )A、y=-x-2 B、y=-x-6 C、y=-x-1 D、y=-x+109. 如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( )
A、5 cm B、 cm C、 cm D、 cm8. 已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的表达式为( )A、y=-x-2 B、y=-x-6 C、y=-x-1 D、y=-x+109. 如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( )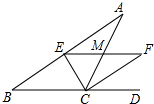 A、75 B、100 C、120 D、12510. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
A、75 B、100 C、120 D、12510. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )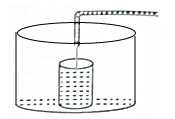 A、
A、 B、
B、 C、
C、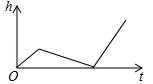 D、
D、
二、填空题
-
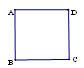
11. 若二次根式 有意义,则x的取值范围是 .12. a、b、c是△ABC三边的长,化简 +|c-a-b|= .13. 命题“全等三角形的对应角相等”的逆命题是这个逆命题是 (填“真”或“假”)14. 如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点A的坐标是(-1,4),则点C的坐标是 .
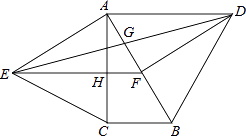
 15. 如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
15. 如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH= BD
其中正确结论的为(请将所有正确的序号都填上).
三、解答题
-
16. 若a=2+ ,b=2- ,求 的值.17. 如图,ABCD是平行四边形,延长AB到E,延长CD到F,使BE=DF,连接EF分别交BC、AD于点G、H,求证:EG=FH.
 18. 已知一次函数y=kx+b的图象经过点(3,5)与(-4,-9).
18. 已知一次函数y=kx+b的图象经过点(3,5)与(-4,-9).
(1)、求这个一次函数的解析式;(2)、求关于x的不等式kx+b≤5的解集.
19. 如图,BD是矩形ABCD的一条对角线.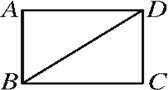 (1)、作BD的垂直平分线EF , 分别交AD , BC于点E , F , 垂足为点O;(要求用尺规作图,保留作图痕迹,不要求写作法)(2)、在(1)中,连接BE和DF , 求证:四边形DEBF是菱形20. 某校为选拔一名选手参加“美丽江门,我为侨乡做代言”主题演讲比赛,经研究,按下图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整),下表是李明、张华在选拔赛中的得分情况:
(1)、作BD的垂直平分线EF , 分别交AD , BC于点E , F , 垂足为点O;(要求用尺规作图,保留作图痕迹,不要求写作法)(2)、在(1)中,连接BE和DF , 求证:四边形DEBF是菱形20. 某校为选拔一名选手参加“美丽江门,我为侨乡做代言”主题演讲比赛,经研究,按下图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整),下表是李明、张华在选拔赛中的得分情况:
服装
普通话
主题
演讲技巧
李明
85
70
80
85
张华
90
75
75
80
结合以上信息,回答下列问题:
(1)、求服装项目在选手考评中的权数;(2)、根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽江门,我为侨乡做代言”主题演讲比赛,并说明理由.21. 如图,△ABC的边AB=8,BC=5,AC=7.求BC边上的高. 22. 如图,点E、F分别在矩形ABCD的边BC、AD上,把这个矩形沿EF折叠后,点D恰好落在BC边上的G点处,且∠AFG=60°
22. 如图,点E、F分别在矩形ABCD的边BC、AD上,把这个矩形沿EF折叠后,点D恰好落在BC边上的G点处,且∠AFG=60°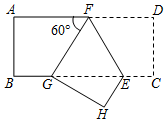 (1)、求证:GE=2EC;(2)、连接CH、DG,试证明:CH∥DG.23. 某公司把一批货物运往外地,有两种运输方案可供选择.
(1)、求证:GE=2EC;(2)、连接CH、DG,试证明:CH∥DG.23. 某公司把一批货物运往外地,有两种运输方案可供选择.方案一:使用快递公司的邮车运输,装卸收费400元,另外每千米再回收4元;
方案二:使用快递公司的火车运输,装卸收费820元,另外每千米再回收2元.
(1)、分别求邮车、火车运输总费用y1(元)、y2(元)关于运输路程x(km)之间的函数关系式:(2)、如何选择运输方案,运输总费用比较节省?24. 如图,菱形ABCD中,AB=1,∠A=60°,EFGH是矩形,矩形的顶点都在菱形的边上.设AE=AH=x(0<x<1),矩形的面积为S. (1)、求S关于x的函数解析式;(2)、当EFGH是正方形时,求S的值.
(1)、求S关于x的函数解析式;(2)、当EFGH是正方形时,求S的值.