广东省珠海市香洲区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-09-12 类型:期末考试
一、单选题
-
1. -8的立方根是( )A、 B、 C、 D、2. 下面四个图形中, 与 是对顶角的是( )A、
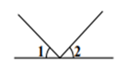 B、
B、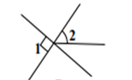 C、
C、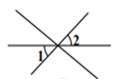 D、
D、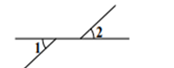 3. 下列调查中,最适宜采用全面调查的是( )A、对我国初中学生视力状况的调查 B、对某班同学一分钟跳绳次数的调查 C、对一批节能灯管使用寿命的调查 D、对珠江现有鱼数量的调查4. 已知a<b,下列不等式变形中正确的是( )A、a-2>b-2 B、 C、3a+1>3b+1 D、-2a>-2b5. 下列计算正确的是( )A、 =±4 B、± =3 C、 =﹣3 D、( )2=36. 如图,两条平行线a,b被直线c所截,若∠2=2∠1,则∠2等于( )
3. 下列调查中,最适宜采用全面调查的是( )A、对我国初中学生视力状况的调查 B、对某班同学一分钟跳绳次数的调查 C、对一批节能灯管使用寿命的调查 D、对珠江现有鱼数量的调查4. 已知a<b,下列不等式变形中正确的是( )A、a-2>b-2 B、 C、3a+1>3b+1 D、-2a>-2b5. 下列计算正确的是( )A、 =±4 B、± =3 C、 =﹣3 D、( )2=36. 如图,两条平行线a,b被直线c所截,若∠2=2∠1,则∠2等于( ) A、60° B、110° C、120° D、150°7. 把方程 改写成用含 的式子表示y的形式,正确的是( )A、 B、 C、 D、8. 如果点P(m+3,m+1)在平面直角坐标系的x轴上,则m=( )A、0 B、-1 C、-2 D、39. 已知关于x、y的二元一次方程组 满足x=y,则k的值为( )A、-1 B、0 C、1 D、210. 一个正数m的平方根是2a+3与1-a,则关于 的不等式 的解集为( )A、 B、 C、 D、
A、60° B、110° C、120° D、150°7. 把方程 改写成用含 的式子表示y的形式,正确的是( )A、 B、 C、 D、8. 如果点P(m+3,m+1)在平面直角坐标系的x轴上,则m=( )A、0 B、-1 C、-2 D、39. 已知关于x、y的二元一次方程组 满足x=y,则k的值为( )A、-1 B、0 C、1 D、210. 一个正数m的平方根是2a+3与1-a,则关于 的不等式 的解集为( )A、 B、 C、 D、二、填空题
-
11. 比较大小:2 (填“﹤”,“=”,“﹥”).12. 一个容量为60的样本最大值为134,最小值为60,取组距为10,则可以分成组.13. 关于x的不等式12-6x≥0的正整数解的和是 .14. 已知二元一次方程组2x-3y-5=0的一组解为 ,则2a-9=15. 如图,有一张四边形纸片ABCD,AD∥BC,将它沿GH折叠,点C落Q处,点D落在AB边上的点E处,若∠GHC=110°,则∠AGE等于
 16. 如图,正方形 的各边分别平行于 轴或 轴,蚂蚁甲和蚂蚁乙都由点 出发,同时沿正方形 的边作环绕运动,蚂蚁甲按顺时针方向以3个单位长度秒的速度作匀速运动,蚂蚁乙按逆时针方向以1个单位长度/秒的速度作匀速运动,则两只蚂蚁出发后的第3次相遇点的坐标是.
16. 如图,正方形 的各边分别平行于 轴或 轴,蚂蚁甲和蚂蚁乙都由点 出发,同时沿正方形 的边作环绕运动,蚂蚁甲按顺时针方向以3个单位长度秒的速度作匀速运动,蚂蚁乙按逆时针方向以1个单位长度/秒的速度作匀速运动,则两只蚂蚁出发后的第3次相遇点的坐标是.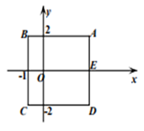
三、解答题
-
17. 计算:18. 解不等式组: .19. 如图, 三个顶点分别是 .将 向下平移4个单位长度,解答下列问题。
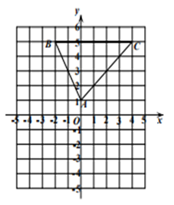 (1)、画出 ,直接写出点 坐标:(2)、连接 ,则 (直接写出结果)20. 如图,8块相同的小长方形恰好拼成一个大的长方形,若小长方形的周长为16厘米.每块小长方形的长和宽分别是多少厘米?
(1)、画出 ,直接写出点 坐标:(2)、连接 ,则 (直接写出结果)20. 如图,8块相同的小长方形恰好拼成一个大的长方形,若小长方形的周长为16厘米.每块小长方形的长和宽分别是多少厘米?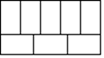 21. 已知A,B,C三点在同一直线上,∠DAE=∠AEB,∠D=∠BEC,
21. 已知A,B,C三点在同一直线上,∠DAE=∠AEB,∠D=∠BEC,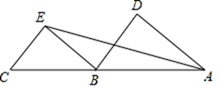 (1)、求证:BD∥CE;(2)、若∠C=70°,∠DAC=50°,求∠DBE的度数.22. 珠海市水务局对某小区居民生活用水情况进行了调査.随机抽取部分家庭进行统计,绘制成如下尚未完成的频数分布表和频率分布直方图.请根据图表,解答下列问题:
(1)、求证:BD∥CE;(2)、若∠C=70°,∠DAC=50°,求∠DBE的度数.22. 珠海市水务局对某小区居民生活用水情况进行了调査.随机抽取部分家庭进行统计,绘制成如下尚未完成的频数分布表和频率分布直方图.请根据图表,解答下列问题:月均用水量(单位:吨
频数
频率
2≤x<3
4
0.08
3≤x<4
a
b
4≤x<5
14
0.28
5≤x<6
9
c
6≤x<7
6
0.12
7≤x<8
5
0.1
合计
d
1.00
 (1)、b= , c= , 并补全频数分布直方图;(2)、为鼓励节约用水用水,现要确定一个用水量标准P(单位:吨),超过这个标准的部分按1.5倍的价格收费,若要使60%的家庭水费支出不受影响,则这个用水量标准P=吨;(3)、根据该样本,请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户?23. 有大小两种货车,3辆大货车与2辆小货车一次可以运货21吨,2辆大货车与4辆小货车一次可以运货22吨.(1)、每辆大货车和每辆小货车一次各可以运货多少吨?(2)、现有这两种货车共10辆,要求一次运货不低于35吨,则其中大货车至少多少辆?(用不等式解答)(3)、日前有23吨货物需要运输,欲租用这两种货车运送,要求全部货物一次运完且每辆车必须装满.已知每辆大货车一次运货租金为300元,每辆小货车一次运货租金为200元,请列出所有的运输方案井求出最少租金.24. 如图1.直线AD∥EF,点B,C分别在EF和AD上,∠A=∠ABC,BD平分∠CBF.
(1)、b= , c= , 并补全频数分布直方图;(2)、为鼓励节约用水用水,现要确定一个用水量标准P(单位:吨),超过这个标准的部分按1.5倍的价格收费,若要使60%的家庭水费支出不受影响,则这个用水量标准P=吨;(3)、根据该样本,请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户?23. 有大小两种货车,3辆大货车与2辆小货车一次可以运货21吨,2辆大货车与4辆小货车一次可以运货22吨.(1)、每辆大货车和每辆小货车一次各可以运货多少吨?(2)、现有这两种货车共10辆,要求一次运货不低于35吨,则其中大货车至少多少辆?(用不等式解答)(3)、日前有23吨货物需要运输,欲租用这两种货车运送,要求全部货物一次运完且每辆车必须装满.已知每辆大货车一次运货租金为300元,每辆小货车一次运货租金为200元,请列出所有的运输方案井求出最少租金.24. 如图1.直线AD∥EF,点B,C分别在EF和AD上,∠A=∠ABC,BD平分∠CBF.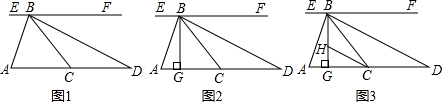 (1)、求证:AB⊥BD;(2)、如图2,BG⊥AD于点G,求证:∠ACB=2∠ABG;(3)、在(2)的条件下,如图3,CH平分∠ACB交BG于点H,设∠ABG=α,请直接写出∠BHC的度数.(用含α的式子表示)25. 如图1,已知点A(-2,0).点D在y轴上,连接AD并将它沿x轴向右平移至BC的位置,且点B坐标为(4,0),连接CD,OD= AB.
(1)、求证:AB⊥BD;(2)、如图2,BG⊥AD于点G,求证:∠ACB=2∠ABG;(3)、在(2)的条件下,如图3,CH平分∠ACB交BG于点H,设∠ABG=α,请直接写出∠BHC的度数.(用含α的式子表示)25. 如图1,已知点A(-2,0).点D在y轴上,连接AD并将它沿x轴向右平移至BC的位置,且点B坐标为(4,0),连接CD,OD= AB.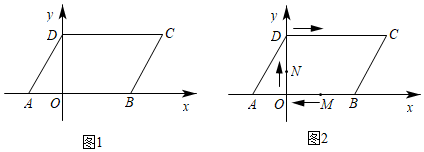 (1)、线段CD的长为,点C的坐标为;(2)、如图2,若点M从点B出发,以1个单位长度/秒的速度沿着x轴向左运动,同时点N从原点O出发,以相同的速度沿折线OD→DC运动(当N到达点C时,两点均停止运动).假设运动时间为t秒.
(1)、线段CD的长为,点C的坐标为;(2)、如图2,若点M从点B出发,以1个单位长度/秒的速度沿着x轴向左运动,同时点N从原点O出发,以相同的速度沿折线OD→DC运动(当N到达点C时,两点均停止运动).假设运动时间为t秒.①t为何值时,MN∥y轴;
②求t为何值时,S△BCM=2S△ADN .