广东省深圳市龙岗区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-09-12 类型:期末考试
一、单选题
-
1. 计算: 的值为( )A、 B、 C、 D、2. 下列标志中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 大肠杆菌的大小为0.0005 0.003毫米,能发酵多种糖类产酸、产气,是人和动物肠道中的正常栖居菌,婴儿出生后即随哺乳进入肠道,与人终身相伴,其中0.0005毫米用科学记数法表示为( )A、 毫米 B、 毫米 C、 毫米 D、 毫米5. 有下列长度的三条线段,其中能组成三角形的是( )A、 、 、 B、 、 、 C、 、 、 D、 、 、6. 一个不透明的袋子中只装有1个黄球和3个红球,它们除颜色外完全相同,从中随机摸出一个球,下列说法正确的是( )A、摸到黄球是不可能事件 B、摸到黄球的概率是 C、摸到红球是随机事件 D、摸到红球是必然事件7. 如图,下列四个条件中,能判断 的是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 大肠杆菌的大小为0.0005 0.003毫米,能发酵多种糖类产酸、产气,是人和动物肠道中的正常栖居菌,婴儿出生后即随哺乳进入肠道,与人终身相伴,其中0.0005毫米用科学记数法表示为( )A、 毫米 B、 毫米 C、 毫米 D、 毫米5. 有下列长度的三条线段,其中能组成三角形的是( )A、 、 、 B、 、 、 C、 、 、 D、 、 、6. 一个不透明的袋子中只装有1个黄球和3个红球,它们除颜色外完全相同,从中随机摸出一个球,下列说法正确的是( )A、摸到黄球是不可能事件 B、摸到黄球的概率是 C、摸到红球是随机事件 D、摸到红球是必然事件7. 如图,下列四个条件中,能判断 的是( ) A、 B、 C、 D、8. 嘉嘉买了6支笔花了9元钱,琪琪买了同样售价的 支笔,还买了单价为5元的三角尺两幅,用 (元)表示琪琪花的总钱数,那么 与 之间的关系式应该是( )A、 B、 C、 D、9. 如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( )
A、 B、 C、 D、8. 嘉嘉买了6支笔花了9元钱,琪琪买了同样售价的 支笔,还买了单价为5元的三角尺两幅,用 (元)表示琪琪花的总钱数,那么 与 之间的关系式应该是( )A、 B、 C、 D、9. 如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( )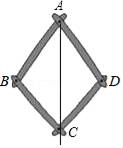 A、SSS B、SAS C、ASA D、AAS10. 已知 , ,则 的值是( )A、49 B、37 C、45 D、3311. 在数学课上,老师提出如下问题:
A、SSS B、SAS C、ASA D、AAS10. 已知 , ,则 的值是( )A、49 B、37 C、45 D、3311. 在数学课上,老师提出如下问题:
小华的作法如下:

老师说:“小华的作法正确”,那么,关于小华第二步作图中①的作法和第二步作图依据的定理或性质②的论述正确的是( )
A、①作 垂直平分 ②垂线段最短 B、①作 平分 ②等腰三角形三线合一 C、①作 垂直平分 ②中垂线性质 D、①作 平分 ②等腰三角形三线合一12. 已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,点P从B出发,沿折线BE-ED-DC匀速运动,运动到点C停止.P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的函数关系图象如图②,则下列结论正确的有( )①a=7②AB=8cm③b=10④当t=10s时,y=12cm2
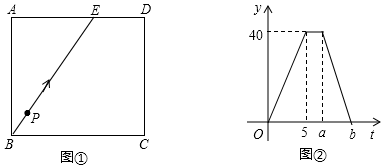 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 等腰三角形的底角为 ,则顶角度数为 .14. 如图,已知AB=AC,用“ASA”定理证明△ABD≌△ACE,还需添加条件 .
 15. 如图,在 中,已知 , , ,则 的度数为 .
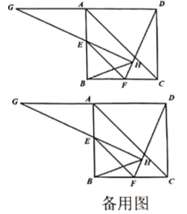
15. 如图,在 中,已知 , , ,则 的度数为 .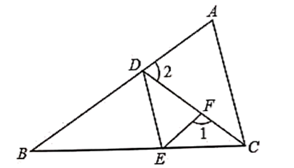 16. 已知长方形 , 点和 点分别在 和 边上,如图将 沿着 折叠以后得到 , 与 相交于点 , 与 相交于点 ,则 与 的数量关系为 .
16. 已知长方形 , 点和 点分别在 和 边上,如图将 沿着 折叠以后得到 , 与 相交于点 , 与 相交于点 ,则 与 的数量关系为 .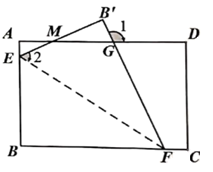
三、解答题
-
17. 计算:(1)、(2)、18. 先化简,再求值: ,其中19. 如图,有一个转盘被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;(③指针指向黄色;④指针不指向黄色,估计各事件的可能性大小,完成下列问题.
 (1)、④事件发生的可能性大小是;(2)、多次实验,指针指向绿色的频率的估计值是;(3)、将这些事件的序号按发生的可能性从小到大的顺序排列为: .20. 某公交车每月的支出费用为4000元,每月的乘车人数 (人)与每月利润(利润=收入费用-支出费用) (元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);
(1)、④事件发生的可能性大小是;(2)、多次实验,指针指向绿色的频率的估计值是;(3)、将这些事件的序号按发生的可能性从小到大的顺序排列为: .20. 某公交车每月的支出费用为4000元,每月的乘车人数 (人)与每月利润(利润=收入费用-支出费用) (元)的变化关系如下表所示(每位乘客的公交票价是固定不变的); (1)、在这个变化过程中,是自变量,是因变量;(填中文)(2)、观察表中数据可知,每月乘客量达到人以上时,该公交车才不会亏损;(3)、请你估计当每月乘车人数为3500人时,每月利润为元?(4)、若5月份想获得利润5000元,则请你估计5月份的乘客量需达人.21. 已知在 与 中, , , 与 交于点 .
(1)、在这个变化过程中,是自变量,是因变量;(填中文)(2)、观察表中数据可知,每月乘客量达到人以上时,该公交车才不会亏损;(3)、请你估计当每月乘车人数为3500人时,每月利润为元?(4)、若5月份想获得利润5000元,则请你估计5月份的乘客量需达人.21. 已知在 与 中, , , 与 交于点 .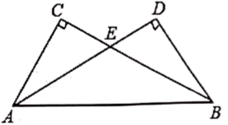 (1)、求证: ;(2)、若 , ,求 的周长.
(1)、求证: ;(2)、若 , ,求 的周长.