广东省深圳市光明区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期：2019-09-12 类型：期末考试
一、单选题
-
1. 石鼓文，秦刻石文字，因其刻石外形似鼓而得名．下列石鼓文，是轴对称的是（ ）A、
B、
C、
D、
2. 2015年诺贝尔医学奖得主中国科学家屠呦呦，发现了一种病毒的长度约为0.00000456毫米，则数据0.00000456用科学记数法表示为（ ）A、0.456×10﹣5 B、4.56×10﹣6 C、4.56×10﹣7 D、45.6×10﹣83. 下列运算正确的是（ ）A、（﹣a2b3）2＝a4b6 B、（﹣a3）•a5＝a8 C、（﹣a2）3＝a5 D、3a2+4a2＝7a44. 下列各组数作为三条线段的长，使它们能构成三角形的一组是（ ）A、2，3，5 B、9，10，15 C、6，7，14 D、4，4，85. 下列事件中是确定事件的是（ ）A、小王参加光明半程马拉松，成绩是第一名 B、小明投篮一次得3分 C、一个月有31天 D、正数大于零6. 下列各式，能用平方差公式计算的是（ ）A、（2a+b）（2b﹣a） B、（ ＋1）（﹣ －1） C、（2a﹣3b）（﹣2a+3b） D、（﹣a﹣2b）（﹣a+2b）7. 如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC ， 交BC于D ， 若BD＝2CD ， 点D到AB的距离为4，则BC的长是（ ）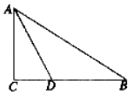
A、4 B、8 C、12 D、168. 一只小花猫在如图的方砖上走来走去，最终停留在阴影方砖上的概率是（ ）
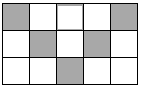A、 B、 C、 D、9. 如图，点E ， 点F在直线AC上，DF＝BE ， ∠AFD＝∠CEB ， 下列条件中不能判断△ADF≌△CBE的是（ ）
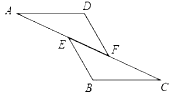A、∠B＝∠D B、AD＝CB C、AE＝CF D、∠A＝∠C10. 如图，CO⊥AB ， 垂足为O ， ∠DOE＝90°，下列结论错误的是（ ）
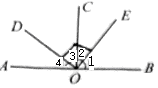A、∠1+∠2＝90° B、∠2+∠3＝90° C、∠1+∠3＝90° D、∠3+∠4＝90°11. 如图，直线a和b被直线c所截，下列条件中不能判断a∥b的是（ ）
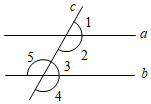A、∠1＝∠3 B、∠2＝∠5 C、∠2+∠4＝180° D、∠2+∠3＝180°12. 如图，已知点D为等腰直角△ABC内一点，∠ACB＝90°，AD＝BD ， ∠BAD＝30°，E为AD延长线上的一点，且CE＝CA ， 若点M在DE上，且DC＝DM ． 则下列结论中：①∠ADB＝120°；②△ADC≌△BDC；③线段DC所在的直线垂直平分线AB；④ME＝BD；正确的有（ ）
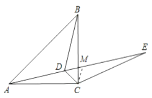A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 计算：2﹣1= ．
14. 用一根长为20cm的铁丝围成一个长方形，若该长方形的一边长为xcm ， 面积为ycm2 ， 则y与x之间的关系式为 ．15. 如图，△ABC中，DE是边AB的垂直平分线，AB＝6，BC＝8，AC＝5，则△ADC的周长是 ．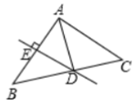
16. 如图，在△ABC中，已知点D ， E ， F ， 分别为BC、AD、CE的中点，且S△ABC＝16，则S阴影＝ ．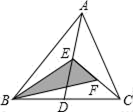
三、解答题
-
17. 计算：(1)、﹣22×（π﹣3.14）0﹣|﹣5|×（﹣1）2019(2)、3x2y2﹣4x3y2÷（﹣2x）+（﹣3xy）218. 先化简，再求值
[（x﹣y）2+（2x+y）（x﹣y）]÷（3x），其中x＝1，y＝﹣2019
19. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，△ABC的顶点均在格点上，直线a为对称轴，点A ， 点C在直线a上．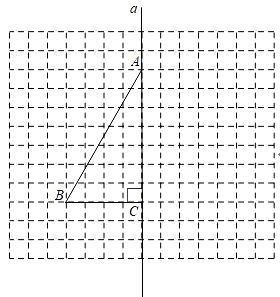
(1)、作△ABC关于直线a的轴对称图形△ADC；(2)、若∠BAC＝35°，则∠BDA＝；(3)、△ABD的面积等于 ．20. 在一个不透明的袋中装有3个绿球，5个红球和若干白球，它们除颜色外其他都相同，将球搅匀，从中任意摸出一个球．(1)、若袋内有4个白球，从中任意摸出一个球，是绿球的概率为 ， 是红球的概率为 ， 是白球的概率为 ．(2)、如果任意摸出一个球是绿球的概率是 ，求袋中有几个白球？21. 2019年5月16日，第十五届文博会在深圳拉开帷幕，周末，小明骑共享单车从家里出发去分会馆参观，途中突然发现钥匙不见了，于是原路折返，在刚才等红绿灯的路口找到了钥匙，便继续前往分会馆，设小明从家里出发到分会场所用的时间为x（分钟），离家的距离为y（米），且x与y的关系示意图如图所示，请根据图中提供的信息回答下列问题：
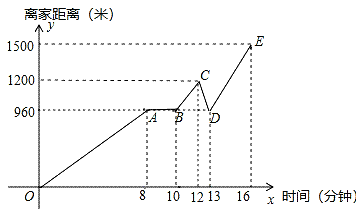(1)、图中自变量是 ． 因变量是 ．(2)、小明等待红绿灯花了分钟．(3)、小明的家距离分会馆米(4)、小明在时间段的骑行速度最快，最快速度是米/分钟．22. 如图，AB∥CD ， 以点A为圆心，小于AC长为半径作圆弧，分别交AB ， AC于E ， F两点，再分别以E ， F为圆心，大于 EF长为半径作圆弧，两条圆弧交于点P ， 作射线AP ， 交CD于点M ，
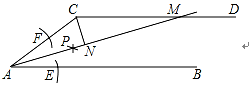(1)、由题意可知，射线AP是；(2)、若∠CMA＝33°，求∠CAB的度数；(3)、若CN⊥AM ， 垂直为N ， 试说明：AN＝MN ．23. 如图，在等腰△ABC中，AB＝AC＝3cm ， ∠B＝30°，点D在BC边上由C向B匀速运动（D不与B、C重合），匀速运动速度为1cm/s ， 连接AD ， 作∠ADE＝30°，DE交线段AC于点E ．
(1)、在此运动过程中，∠BDA逐渐变（填“大”或“小”）；D点运动到图1位置时，∠BDA＝75°，则∠BAD＝ ．(2)、点D运动3s后到达图2位置，求CD的长 ． 此时△ABD和△DCE是否全等，请说明理由；(3)、在点D运动过程中，△ADE的形状也在变化，判断当△ADE是等腰三角形时，∠BDA等于多少度（请直接写出结果）