广东省广州市荔湾区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-09-12 类型:期末考试
一、单选题
-
1. 实数 , , , 中无理数是( )A、 B、 C、 D、2. 为了解某市2018年参加中考的32000名学生的视力情况,抽查了其中1600名学生的视力进行统计分析,下面叙述错误的是( )A、32000名学生的视力情况是总体 B、样本容量是32000 C、1600名学生的视力情况是总体的一个样本 D、以上调查是抽样调查3. 如图,俄罗斯方块游戏中,图形 经过平移使其填补空位,则正确的平移方式是( )
 A、先向右平移5格,再向下平移3格 B、先向右平移4格,再向下平移5格 C、先向右平移4格,再向下平移4格 D、先向右平移3格,再向下平移5格4. 已知点 在第二象限且到 轴的距离为3,到 轴的距离为2,则 点坐标为( )A、 B、 C、 D、5. 一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A、先向右平移5格,再向下平移3格 B、先向右平移4格,再向下平移5格 C、先向右平移4格,再向下平移4格 D、先向右平移3格,再向下平移5格4. 已知点 在第二象限且到 轴的距离为3,到 轴的距离为2,则 点坐标为( )A、 B、 C、 D、5. 一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( ) A、10° B、15° C、18° D、30°6. 已知 ,则下列不等式正确的是( )A、 B、 C、 D、7. 下列说法:①与同一条直线平行的两条直线必平行;②相等的角是对顶角;③在同一平面内,过一点有且只有一条直线与已知直线垂直;④在同一平面内,没有交点的两条直线叫平行线,其中正确命题有( )个A、1 B、2 C、3 D、48. 已知关于x,y的二元一次方程组 的解为 ,则a﹣2b的值是( )A、﹣2 B、2 C、3 D、﹣39. 关于 的不等式 有3个整数解,则 的取值范围是( )A、 B、 C、 D、10. 已知实数 , 同时满足三个条件:① ;② ;③ ,那么实数 的取值范围是( )A、 B、 C、 D、
A、10° B、15° C、18° D、30°6. 已知 ,则下列不等式正确的是( )A、 B、 C、 D、7. 下列说法:①与同一条直线平行的两条直线必平行;②相等的角是对顶角;③在同一平面内,过一点有且只有一条直线与已知直线垂直;④在同一平面内,没有交点的两条直线叫平行线,其中正确命题有( )个A、1 B、2 C、3 D、48. 已知关于x,y的二元一次方程组 的解为 ,则a﹣2b的值是( )A、﹣2 B、2 C、3 D、﹣39. 关于 的不等式 有3个整数解,则 的取值范围是( )A、 B、 C、 D、10. 已知实数 , 同时满足三个条件:① ;② ;③ ,那么实数 的取值范围是( )A、 B、 C、 D、二、填空题
-
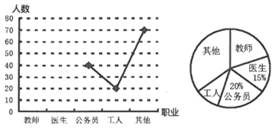
11. 比较大小: 填“ ”、“ ”或“ ” .12. 在平面直角坐标系中,点 的坐标为 ,将点 沿 轴的正方向平移 个单位后,得到的对应点的坐标为 ,则 .13. 某中学开展以“我最喜欢的职业”为主题的调查活动,根据数据绘制的不完整统计图如图所示,图中工人部分所对应的圆心角为.
 14. 如图,把一张长方形纸片 沿 折叠后,点 、 分别落在 、 的位置上,若 ,则 .
14. 如图,把一张长方形纸片 沿 折叠后,点 、 分别落在 、 的位置上,若 ,则 .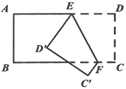 15. 对于任意实数 、 ,定义关于“ ”的一种运算如下: ,例如: .若 , ,则 = , .
15. 对于任意实数 、 ,定义关于“ ”的一种运算如下: ,例如: .若 , ,则 = , .三、解答题
-
16.(1)、计算: ;(2)、解方程组:17. 解不等式组 ,并把解集在数轴上表示出来.18. 如图,△ABC经过平移后,顶点A平移到了A/(-1,3);
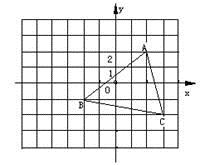 (1)、画出平移后的△A′B′C′;(2)、求出△A′B′C′的面积.19. 为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表:
(1)、画出平移后的△A′B′C′;(2)、求出△A′B′C′的面积.19. 为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表:零花钱数额 元
人数(频数)
频率
6
0.15
12
0.30
16
0.40
0.10
2
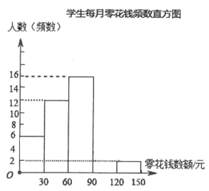
请根据以下图表,解答下列问题:
(1)、这次被调查的人数共有人, ;(2)、计算并补全频数分布直方图;(3)、请估计该校1500名学生中每月零花钱数额低于90的人数.20. 如图,在四边形 中, , , 、 分别是 和 的平分线.求证: . 21. 某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.(1)、求每辆大客车和每辆小客车的乘客座位数;(2)、由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.22. 如图,已知 ,直线 分别与 、 交于点 、点 .
21. 某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.(1)、求每辆大客车和每辆小客车的乘客座位数;(2)、由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.22. 如图,已知 ,直线 分别与 、 交于点 、点 .

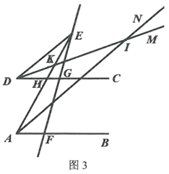 (1)、如图1,当点 在线段 上,若 , ,则 °;(2)、如图2,当点 在线段 的延长线上, 与 交于点 ,则 、 、 之间满足怎样的关系,请证明你的结论;(3)、如图3,在(2)的条件下, 平分 ,交 于点 ,射线 将 分成 ,且与 交于点 ,若 , ,求 的度数.
(1)、如图1,当点 在线段 上,若 , ,则 °;(2)、如图2,当点 在线段 的延长线上, 与 交于点 ,则 、 、 之间满足怎样的关系,请证明你的结论;(3)、如图3,在(2)的条件下, 平分 ,交 于点 ,射线 将 分成 ,且与 交于点 ,若 , ,求 的度数.