广东省广州市花都区2017--2018学年七年级下学期数学期末考试试卷
试卷更新日期:2019-09-12 类型:期末考试
一、单选题
-
1. 若(1,2)表示教室里第1列第2排的位置,则教室里第2列第3排的位置表示为( )A、(2,1) B、(3,3) C、(2,3) D、(3,2)2. 在平面直角坐标系中,点(5,3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 不等式x>3在数轴上表示正确的是( )A、
 B、
B、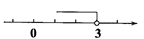 C、
C、 D、
D、 4. 下列各数中,有理数是( )A、 B、 C、3.14 D、5. 下列调查中,最适合采用全面调查(普查)的是( )A、对广州市某校七(1)班同学的视力情况的调查 B、对广州市市民知晓“礼让行人”交通新规情况的调查 C、对广州市中学生观看电影《厉害了,我的国》情况的调查 D、对广州市中学生每周课外阅读时间情况的调查6. 如图,能判定直线a∥b的条件是( )
4. 下列各数中,有理数是( )A、 B、 C、3.14 D、5. 下列调查中,最适合采用全面调查(普查)的是( )A、对广州市某校七(1)班同学的视力情况的调查 B、对广州市市民知晓“礼让行人”交通新规情况的调查 C、对广州市中学生观看电影《厉害了,我的国》情况的调查 D、对广州市中学生每周课外阅读时间情况的调查6. 如图,能判定直线a∥b的条件是( )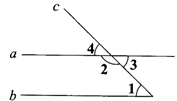 A、∠2+∠4=180° B、∠3=∠4 C、∠1+∠4=90° D、∠1=∠47. 若a<b,则下列式子一定成立的是( )A、a+c>b+c B、a-c<b-c C、ac<bc D、8. 估算 在下列哪两个整数之间( )A、1,2 B、2,3 C、3,4 D、4,59. 如果方程组 的解为 ,那么“口”和“△”所表示的数分别是( )A、14,4 B、11,1 C、9,-1 D、6,-410. 如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )
A、∠2+∠4=180° B、∠3=∠4 C、∠1+∠4=90° D、∠1=∠47. 若a<b,则下列式子一定成立的是( )A、a+c>b+c B、a-c<b-c C、ac<bc D、8. 估算 在下列哪两个整数之间( )A、1,2 B、2,3 C、3,4 D、4,59. 如果方程组 的解为 ,那么“口”和“△”所表示的数分别是( )A、14,4 B、11,1 C、9,-1 D、6,-410. 如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( ) A、∠1=∠2 B、∠1=2∠2 C、∠1=3∠2 D、∠1=4∠2
A、∠1=∠2 B、∠1=2∠2 C、∠1=3∠2 D、∠1=4∠2二、填空题
-
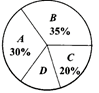
11. 4的算术平方根是 , 9的平方根是 , ﹣27的立方根是 .12. 某校全体同学的综合素质评价的等级统计如图所示,其中评价为C等级所在扇形的圆心角是度.
 13. 如图,将△ABE向右平移3cm得到△DCF,若BE=8cm,则CE=cm.
13. 如图,将△ABE向右平移3cm得到△DCF,若BE=8cm,则CE=cm.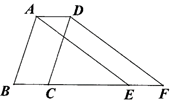 14. 下列命题:①若∠1=∠2,∠2=∠3,则∠1=∠3;②若|a|=|b|,则a=b;③内错角相等;④对顶角相等.其中真命题的是(填写序号)15. 已知二元一次方程2x-3y=5的一组解为 ,则2a-3b+3=.16. 如图,在平面直角坐标系中,动点P按图中箭头所示方向从原点出发,第1次运动到P1(1,1),第2次接着运动到点P2(2,0),第3次接着运动到点P3(3,-2),…,按这的运动规律,点P2019的坐标是.
14. 下列命题:①若∠1=∠2,∠2=∠3,则∠1=∠3;②若|a|=|b|,则a=b;③内错角相等;④对顶角相等.其中真命题的是(填写序号)15. 已知二元一次方程2x-3y=5的一组解为 ,则2a-3b+3=.16. 如图,在平面直角坐标系中,动点P按图中箭头所示方向从原点出发,第1次运动到P1(1,1),第2次接着运动到点P2(2,0),第3次接着运动到点P3(3,-2),…,按这的运动规律,点P2019的坐标是.
三、解答题
-
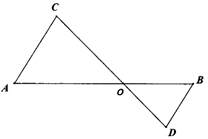
17. 计算(1)、(2)、18. 如图,AB和CD相交于点O,∠A=∠B,∠C=75°求∠D的度数.
 19. 解方程组 .20. 解不等式组 ,并在数轴上表示解集.21. 如图,把△ABC先向上平移3个单位长度,再向右平移2个单位长度,得到△A1B1C1.
19. 解方程组 .20. 解不等式组 ,并在数轴上表示解集.21. 如图,把△ABC先向上平移3个单位长度,再向右平移2个单位长度,得到△A1B1C1. (1)、在图中画出△A1B1C1 , 并写出点A1、B1、C1的坐标;(2)、连接A1A、C1C,则四边形A1ACC1的面积为.22. 某学校七年级举行“每天锻炼一小时,健康生活一辈子”为主题的一分钟跳绳大赛,校团委组织了全级1000名学生参加为了解本次大赛的成绩,校团委随机抽取了其中100名学生的成绩(成绩取整数,总分100分)作为样本进行统计,制成如下不完整的统计图表根据所给信息,解答下列问题:
(1)、在图中画出△A1B1C1 , 并写出点A1、B1、C1的坐标;(2)、连接A1A、C1C,则四边形A1ACC1的面积为.22. 某学校七年级举行“每天锻炼一小时,健康生活一辈子”为主题的一分钟跳绳大赛,校团委组织了全级1000名学生参加为了解本次大赛的成绩,校团委随机抽取了其中100名学生的成绩(成绩取整数,总分100分)作为样本进行统计,制成如下不完整的统计图表根据所给信息,解答下列问题:成绩x/分 频数/人 百分比 50≤x<60 5 5% 60≤x<70 15 15% 70≤x<80 20 20% 80≤x<90 m 35% 90≤x<100 25 n  (1)、m= , n=.(2)、补全频数分布直方图;(3)、若成绩在80分以上(包括80分)为“优”,请你估计该校七年级参加本次比赛的1000名学生中成绩是“优”的有多少人23. 如图,已知∠1=∠2,∠BAC=∠DEC,试判断AD与FG的位置关系,并说明理由.
(1)、m= , n=.(2)、补全频数分布直方图;(3)、若成绩在80分以上(包括80分)为“优”,请你估计该校七年级参加本次比赛的1000名学生中成绩是“优”的有多少人23. 如图,已知∠1=∠2,∠BAC=∠DEC,试判断AD与FG的位置关系,并说明理由.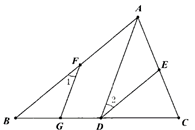 24. 为引导学生“爱读书,多读书,读好书”,某校七(2)班决定购买A、B两种书籍.若购买A种书籍1本和B种书籍3本,共需要180元;若购买A种书籍3本和B种书籍1本,共需要140元.(1)、求A、B两种书籍每本各需多少元?(2)、该班根据实际情况,要求购买A、B两种书籍总费用不超过700元,并且购买B种书籍的数量是A种书籍的 ,求该班本次购买A、B两种书籍有哪几种方案?25. 如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
24. 为引导学生“爱读书,多读书,读好书”,某校七(2)班决定购买A、B两种书籍.若购买A种书籍1本和B种书籍3本,共需要180元;若购买A种书籍3本和B种书籍1本,共需要140元.(1)、求A、B两种书籍每本各需多少元?(2)、该班根据实际情况,要求购买A、B两种书籍总费用不超过700元,并且购买B种书籍的数量是A种书籍的 ,求该班本次购买A、B两种书籍有哪几种方案?25. 如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.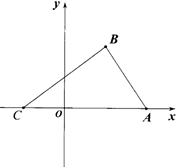 (1)、直接写出点C的坐标.(2)、在y轴上是否存在点P,使得S△POB= S△ABC若存在,求出点P的坐标;若不存在,请说明理由.(3)、把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.
(1)、直接写出点C的坐标.(2)、在y轴上是否存在点P,使得S△POB= S△ABC若存在,求出点P的坐标;若不存在,请说明理由.(3)、把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.