初中数学浙教版九年级上册第二章 简单事件的概率 章末检测
试卷更新日期:2019-09-05 类型:单元试卷
一、单选题
-
1. 下列事件中,是随机事件的是( )A、任意画一个三角形,其内角和是360° B、任意抛一枚图钉,钉尖着地 C、通常加热到100℃时,水沸腾 D、太阳从东方升起2. 下列语句描述的事件中,是随机事件的为( )A、水能载舟,亦能覆舟 B、只手遮天,偷天换日 C、瓜熟蒂落,水到渠成 D、心想事成,万事如意3. 下列说法中,正确的是( )A、不可能事件发生的概率为0 B、 随机事件发生的概率为 C、概率很小的事件不可能发生 D、投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次4. 一个布袋里装有2个红球,3个黑球,4个白球,它们除颜色外都相同,从中任意摸出1个球,则下列事件中,发生可能性最大的是( )
A、摸出的是白球 B、摸出的是黑球 C、摸出的是红球 D、摸出的是绿球5. 抛掷一枚质地均匀的硬币,正面朝上的概率为0.5,下列说法正确的是( )A、连续抛掷2次必有1次正面朝上 B、连续抛掷10次不可能都正面朝上 C、大量反复抛掷每100次出现正面朝上50次 D、通过抛掷硬币确定谁先发球的比赛规则是公平的6. 下列计算① ② ③ ④ ⑤ ,
其中任意抽取一个,运算结果正确的概率是( )
A、 B、 C、 D、7. 如图,有一电路AB是由图示的开关控制,闭合a,b,c,d,e五个开关中的任意两个开关,使电路形成通路,则使电路形成通路的概率是( )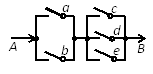 A、 B、 C、 D、8. 甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( )
A、 B、 C、 D、8. 甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( )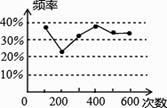 A、掷一枚质地均匀的正六面体的骰子,向上的一面点数是1点的概率 B、抛一枚质地均匀的硬币,出现正面朝上的概率 C、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率 D、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率9. 在围棋盒中有x颗白色棋子和y颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是 .如果再往盒中放进6颗黑色棋子,取得白色棋子的概率是 ,则原来盒中有白色棋子( )A、8颗 B、6颗 C、4颗 D、2颗10. 甲乙两人轮流在黑板上写下不超过
A、掷一枚质地均匀的正六面体的骰子,向上的一面点数是1点的概率 B、抛一枚质地均匀的硬币,出现正面朝上的概率 C、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率 D、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率9. 在围棋盒中有x颗白色棋子和y颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是 .如果再往盒中放进6颗黑色棋子,取得白色棋子的概率是 ,则原来盒中有白色棋子( )A、8颗 B、6颗 C、4颗 D、2颗10. 甲乙两人轮流在黑板上写下不超过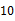 的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
A、10 B、9 C、8 D、6二、填空题
-
11. 在线段AB上任取三点x1、x2、x3 , 则x2位于x1与x3之间的可能性(填写“大于”、“小于”或“等于”)x2位于两端的可能性.
12. 一个不透明的盒子中装有6张生肖邮票,其中有3张“猴票”,2张“鸡票”和1张“狗票”,这些邮票除了画面内容外其他都相同,从中随机摸出一张邮票,恰好是“鸡票”的可能性为 . 13. 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC不是直角三角形的概率是 .
13. 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC不是直角三角形的概率是 . 14. 若正整数n使得在计算n+(n+1)+(n+2)的过程中,各数位均不产生进位现象,则称n为“本位数”.例如2和30是“本位数”,而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中,任意抽取一个数,抽到偶数的概率为.
14. 若正整数n使得在计算n+(n+1)+(n+2)的过程中,各数位均不产生进位现象,则称n为“本位数”.例如2和30是“本位数”,而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中,任意抽取一个数,抽到偶数的概率为.
15. 若质量抽检时任抽一件西服成品为合格品的概率为0.9,则200件西服中大约有合格品.三、综合题
-
16. 下列事件,哪些是必然发生的事件?哪些是不可能发生的事件?哪些是随机事件?(1)、有一副洗好的只有数字1~10的10张扑克牌。
①任意抽取一张牌,它比6小;
②一次任意抽出两张牌,它们的和是24;
③一次任意抽出两张牌,它们的和不小于2。
(2)、在一个不透明的口袋中,装有10个大小和外形-模一样的小球,其中有5个红球,3个蓝球,2个白球,并在口袋中搅匀①从口袋中摸出一个球,它们恰好是白球;
②从口袋中任意抽出2个球,它们恰好是白球;
③从口袋中一次摸出3个球,它们的颜色分别是红色、蓝色、白色;
④从口袋中一次摸出5个球,它们恰好是1个红色、1个蓝色和3个白色。
17. 图2是中国象棋棋盘的一部分,图中红方有两个马,黑方有三个卒子和一个炮,按照中国象棋中马的行走规则(马走日字,例如:按图1中的箭头方向走),红方的马现在走一步能吃到黑方棋子的概率是多少? 18. 一次抽奖活动设置如下的翻奖牌,翻奖牌的正面、背面如下,如果你只能在9个数字中选中一个翻牌,请解决下面的问题:
18. 一次抽奖活动设置如下的翻奖牌,翻奖牌的正面、背面如下,如果你只能在9个数字中选中一个翻牌,请解决下面的问题: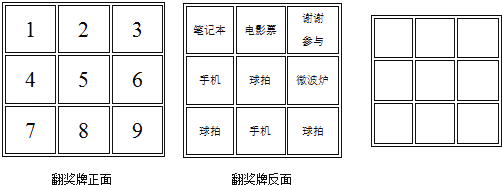 (1)、直接写出抽到“手机”奖品的可能性的大小;
(1)、直接写出抽到“手机”奖品的可能性的大小;
(2)、若第一次没有抽到“手机”奖品,请求出第二次抽到“手机”奖品的可能性的大小;
(3)、请你根据题意设计翻奖牌反面的奖品,包含(手机、微波炉、球拍、电影票,谢谢参与)使得最后抽到“球拍”的可能性大小是 .
19. 一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是年平的 将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下 由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:实验次数
20
40
60
80
100
120
140
160
“兵”字面朝上频数
14
38
47
52
66
78
88
相应频率
(1)、请将数据补充完整;(2)、画出“兵”字面朝上的频率分布折线图; (3)、如果实验继续进行下去,根据上表的数据,这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?20. 如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
(3)、如果实验继续进行下去,根据上表的数据,这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?20. 如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等. (1)、随机转动转盘一次,停止后(若指针落在分割线上,则重新转动,直至指向数字),指针指向数字1的概率是多少?(直接写出结果)(2)、小丽和小芳利用此转盘做游戏,游戏规则如下:自由转动转盘两次(若指针落在分割线上,则重转,直至指向数字),如果指针两次所指的数字之和为偶数,则小丽胜;否则,小芳胜.你认为对双方公平吗?请说明理由.
(1)、随机转动转盘一次,停止后(若指针落在分割线上,则重新转动,直至指向数字),指针指向数字1的概率是多少?(直接写出结果)(2)、小丽和小芳利用此转盘做游戏,游戏规则如下:自由转动转盘两次(若指针落在分割线上,则重转,直至指向数字),如果指针两次所指的数字之和为偶数,则小丽胜;否则,小芳胜.你认为对双方公平吗?请说明理由.
21. 经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转.由于该十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为 ,向左转和直行的频率均为 .(1)、假设平均每天通过该路口的汽车为5000辆,求汽车在此左转、右转、直行的车辆各是多少辆;(2)、目前在此路口,汽车左转、右转、直行的绿灯亮的时间均为30秒,在绿灯总时间不变的条件下,为了缓解交通拥挤,请你利用概率的知识对此路口三个方向的绿灯亮的时间做出合理的调整.