初中数学浙教版九年级上册2.3 用频率估计概率 同步训练
试卷更新日期：2019-09-05 类型：同步测试
一、基础夯实
-
1. 在一个不透明的袋子中有20个除颜色外均相同的小球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.4，由此可估计袋中红球的个数约为（ ）A、4 B、6 C、8 D、122. 如图，两个转盘A，B都被分成了3个全等的扇形，在每一扇形内均标有不同的自然数，固定指针，同时转动转盘A，B，两个转盘停止后观察两个指针所指扇形内的数字（若指针停在扇形的边线上，当作指向上边的扇形）.小明每转动一次就记录数据，并算出两数之和，其中“和为7”的频数及频率如下表：
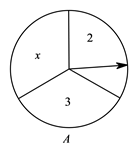
如果实验继续进行下去，根据上表数据，出现“和为7”的频率将稳定在它的概率附近，估计出现“和为7”的概率为（ ）
A、0.33 B、0.34 C、0.20 D、0.353. 在一个不透明的布袋中装有红色、黄色的球共40个，除颜色外其它完全相同．通过多次摸球试验后发现摸到黄色球的频率稳定在25%左右，则口袋中黄色球可能有个．4. 在100个数据中，用适当方法抽取50个样本进行统计，在频数分布表中，54.5～57.5这一组的频率是0.2，那么估计总体数据落在54.5～57.5之间的约有个．5. 林业部门要考察某种幼树在一定条件下的移植成活率，下图是这种幼树在移植过程中幼树成活率的统计图：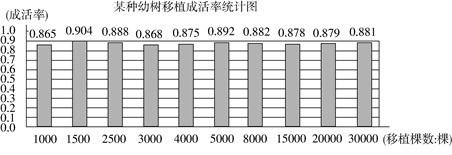
估计该种幼树在此条件下移植成活的概率为（结果精确到0.01）．
6. 如图，显示的是用计算机模拟随机投掷一枚图钉的某次试验的结果.小明根据试验结果推断：随着重复试验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，就可以估计“钉尖向上”的概率是0.618.你认为小明的推断是（填写“正确”或“错误”）的.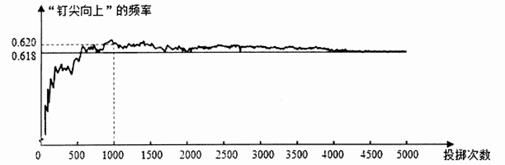
二、中考演练
-
7. 一个不透明的袋子中有三个完全相同的小球，把它们分别标号为1，2，3，随机摸出一个小球，记下标号后放回，再随机摸出一个小球并记下标号，两次摸出的小球标号的和是偶数的概率是（ ）A、 B、 C、 D、8. 某小组做“用频率估计概率”的实验时，绘出的某一结果出现的频率折线图，则符合这一结果的实验可能是（ ）
A、抛一枚硬币，出现正面朝上 B、掷一个正六面体的骰子，出现3点朝上 C、一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃 D、从一个装有2个红球1个黑球的袋子中任取一球，取到的是黑球9. 柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下，对某植物种子发芽率进行研究时所得到的数据：种子数n
30
75
130
210
480
856
1250
2300
发芽数m
28
72
125
200
457
814
1187
2185
发芽频率
0.9333
0.9600
0.9615
0.9524
0.9521
0.9509
0.9496
0.9500
依据上面的数据可以估计，这种植物种子在该实验条件下发芽的概率约是(结果精确到0.01).
10. 为了解某地七年级学生身高情况，随机抽取部分学生，测得他们的身高(单位：cm)，并绘制了如下两幅不完整的统计图，请结合图中提供的信息，解答下列问题．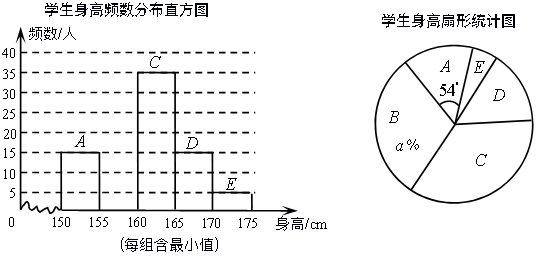
(1)、填空：样本容量为 ， a=；(2)、把频数分布直方图补充完整；(3)、若从该地随机抽取1名学生，估计这名学生身高低于160cm的概率．11. 如图表示的是某班部分同学衣服上口袋的数目．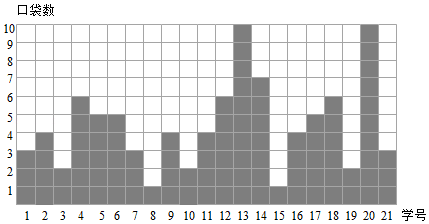
(1)、从图中给出的信息得到学生衣服上口袋数目的中位数为 ， 众数为 ．(2)、根据如图信息，在给出的图表中绘制频数条形统计图，由此估计该班学生衣服上口袋数目为 的概率．三、提高特训
-
12. 一个暗箱中放有除颜色外其他完全相同的m个红球，6个黄球，3个白球现将球搅匀后，任意摸出1个球记下颜色，再放回暗箱，通过大量重复试验后发现，摸到黄球的频率稳定在 附近，由此可以估算m的值是 ．13. 在一个不透明的塑料袋中装有红色、白色球共40个，除颜色外其它都相同，小明通过多次摸球实验后发现，其中摸到红色球的频率稳定在15%左右，则口袋中白色球可能（ ）A、4个 B、6个 C、34个 D、36个14. 某工厂对一批灯泡的质量进行随机抽查，见下表：
抽取灯泡数a
40
100
150
500
1000
1500
优等品数b
36
92
145
474
950
1427
优等品频率
(1)、计算表中的优等品的频率（精确到0.001）(2)、根据抽查的灯泡优等品的频率，估计这批灯泡优等品的概率（精确到0.01）15. 在一个不透明的袋子里有1个红球，1个黄球和n个白球，它们除颜色外其余都相同．(1)、从这个袋子里摸出一个球，记录其颜色，然后放回，摇均匀后，重复该实验，经过大量实验后，发现摸到白球的频率稳定于0.5左右，求n的值；(2)、在（1）的条件下，先从这个袋中摸出一个球，记录其颜色，放回，摇均匀后，再从袋中摸出一个球，记录其颜色．请用画树状图或者列表的方法，求出先后两次摸出不同颜色的两个球的概率．16. 在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只，某学习小组做摸球实验.将球搅匀后从中随机摸出一个球，记下颜色，再把它放回袋中，不断重复，下表是活动进行中记下的一组数据摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
58
96
116
295
484
601
摸到白球的频率
0.58
0.64
0.58
0.59
0.605
0.601
(1)、请你估计，当n很大时，摸到白球的频率将会接近(精确到0.1).(2)、假如你去摸一次，你摸到白球的概率是 ， 摸到黑球的概率是.(3)、试估算口袋中黑、白两种颜色的球有多少只.