备考2020年高考数学一轮复习:23 平面向量的概念及线性运算
试卷更新日期:2019-09-04 类型:一轮复习
一、单选题
-
1. 已知 为非零不共线向量,向量 与 共线,则 ( )A、 B、 C、 D、82. ( )A、 B、 C、 D、3. 如图,△ABC中,E,F分别是BC,AC边的中点,AE与BF相交于点G,则 =( )
 A、 B、 C、 D、4. 如图,在 中, , ,若 ,则 的值为( )
A、 B、 C、 D、4. 如图,在 中, , ,若 ,则 的值为( )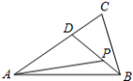 A、 B、 C、 D、5. 在 中, 为 边上的中线, 为 的中点,则 ( )A、 B、 C、 D、6. 在平行四边形 中,下列结论错误的是( )A、 B、 C、 D、7. 在 中, , .若点 满足 ,则 ( )A、 B、 C、 D、8. 在 中, ,则 =( )A、 B、 C、 D、9. 在等腰梯形ABCD中, ,点E是线段BC的中点,若 ,则A、 B、 C、 D、10. 已知 为平行四边形,若向量 , ,则向量 为( )
A、 B、 C、 D、5. 在 中, 为 边上的中线, 为 的中点,则 ( )A、 B、 C、 D、6. 在平行四边形 中,下列结论错误的是( )A、 B、 C、 D、7. 在 中, , .若点 满足 ,则 ( )A、 B、 C、 D、8. 在 中, ,则 =( )A、 B、 C、 D、9. 在等腰梯形ABCD中, ,点E是线段BC的中点,若 ,则A、 B、 C、 D、10. 已知 为平行四边形,若向量 , ,则向量 为( )
A、 B、 C、 D、11. 设 是两个单位向量,则下列结论中正确的是( )A、 B、 C、 D、12. 向量 化简后等于( )A、 B、 C、 D、二、填空题
-
13. 已知向量 满足: , ,当 取最大值时, .14. 在 中,已知 是 延长线上一点,若 ,点 为线段 的中点, ,则 .15. 若 与 是互为相反向量,则 .16. 在平行四边形 中,点 是 的中点,点 是 的中点,记 , ,用 , 表示 ,则 .17. 已知单位向量 与 的夹角是 ,则 .
三、解答题

