备考2020年高考数学一轮复习:19 函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用
试卷更新日期:2019-09-04 类型:一轮复习
一、单选题
-
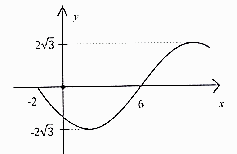
1. 已知函数 是奇函数,且 的最小正周期为 ,将 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为 .若 ,则 ( )A、-2 B、- C、 D、22. 将函数 的图象向右平移 个单位长度得到 图象,则函数的解析式是( )A、 B、 C、 D、3. 要得到 的图象,只要将函数 的图象( )A、向左平移 单位 B、向右平移 单位 C、向左平移 单位 D、向右平移 单位4. 数 ,若将 的图象向左平移 个单位后所得函数的图象关于 轴对称,则 ( )A、 B、 C、 D、5. 函数 的部分图象如图所示,则函数 的解析式为( ).
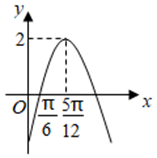 A、 B、 C、 D、6. 将函数 的图象上所有的点向右平移 个单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得图象的解析式为( )A、 B、 C、 D、7. 函数 ( 是常数, )的部分图像如图所示,则 ( )
A、 B、 C、 D、6. 将函数 的图象上所有的点向右平移 个单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得图象的解析式为( )A、 B、 C、 D、7. 函数 ( 是常数, )的部分图像如图所示,则 ( )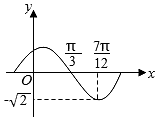 A、 B、 C、 D、8. 已知函数 ,且此函数的图象如图所示,由点 的坐标是( )
A、 B、 C、 D、8. 已知函数 ,且此函数的图象如图所示,由点 的坐标是( )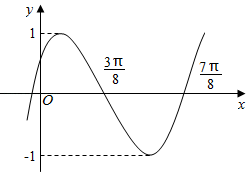 A、 B、 C、 D、9. 将函数f(x)=sin(ωx+ )(0>0)的图象向右平移 个单位长度,得到的图象关于y轴对称,则ω的最小值为( )A、7 B、6 C、5 D、410. 已知 sinα+ cosα=2,则tanα=( )A、- B、 C、- D、11. 已知曲线C1:y=cos x,C2:y=sin (2x+ ),则下面结论正确的是( )A、把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C2 B、把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线C2 C、把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C2 D、把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线C212. 已知函数 , ,要得到函数 的图象,只需将函数 的图象上的所有点( )A、横坐标缩短为原来的 ,再向右平移 个单位得到 B、横坐标缩短为原来的 ,再向右平移 个单位得到 C、横坐标伸长为原来的2倍,再向右平移 个单位得到 D、横坐标伸长为原来的2倍,再向右平移 个单位得到
A、 B、 C、 D、9. 将函数f(x)=sin(ωx+ )(0>0)的图象向右平移 个单位长度,得到的图象关于y轴对称,则ω的最小值为( )A、7 B、6 C、5 D、410. 已知 sinα+ cosα=2,则tanα=( )A、- B、 C、- D、11. 已知曲线C1:y=cos x,C2:y=sin (2x+ ),则下面结论正确的是( )A、把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C2 B、把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线C2 C、把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C2 D、把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线C212. 已知函数 , ,要得到函数 的图象,只需将函数 的图象上的所有点( )A、横坐标缩短为原来的 ,再向右平移 个单位得到 B、横坐标缩短为原来的 ,再向右平移 个单位得到 C、横坐标伸长为原来的2倍,再向右平移 个单位得到 D、横坐标伸长为原来的2倍,再向右平移 个单位得到二、填空题
-
13. 函数f(x)=Asin( x+ )的部分图象如图,其中A>0, >0,0< < .则 = ; tan = .
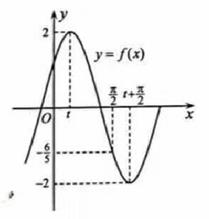 14. 将函数 的图象向右平移 ( )个单位长度后,其函数图象关于 轴对称,则 的最小值为 .15. 已知函数 是由 向左平移 个单位得到的,则 .16. 先将函数 的图象向右平移 个单位,再向上平移 个单位后,得到函数 的图象,函数 的解析式为.17. 的最小正周期为 , 为了得到函数 的图象,可以将函数 的图象向左最小移动个单位
14. 将函数 的图象向右平移 ( )个单位长度后,其函数图象关于 轴对称,则 的最小值为 .15. 已知函数 是由 向左平移 个单位得到的,则 .16. 先将函数 的图象向右平移 个单位,再向上平移 个单位后,得到函数 的图象,函数 的解析式为.17. 的最小正周期为 , 为了得到函数 的图象,可以将函数 的图象向左最小移动个单位三、解答题
-
18. 向量 ,设函数 .

(Ⅰ)求 的表达式并化简;
(Ⅱ)写出 的最小正周期并在右边直角坐标中画出函数 在区间 内的草图;
(Ⅲ)若方程 在 上有两个根 ,求m的取值范围及 的值.
19. 已知函数y=sin(x+ ).(1)、试用“五点法”画出它的图象;(2)、求它的振幅、周期和初相:(3)、根据图象写出它的单调递减区间.