江苏省南通市如皋2018-2019学年高一上学期数学教学质量调研(三)
试卷更新日期:2019-09-04 类型:月考试卷
一、单选题
-
1. 已知集合 , ,若 ,则 ( )A、 B、 C、 D、2. 已知扇形的圆心角为 ,半径为6,则扇形的面积为( )A、 B、 C、 D、3. 函数 的定义域为( )A、 B、 C、 D、4. 已知向量 , ,若向量 与 平行,则实数 的值为( )
A、2 B、-1 C、-2 D、15. 下列函数中,既是偶函数,又在区间 上单调递增的函数是( )A、 B、 C、 D、6. 已知 ,且 与 夹角为 ,则向量 与 的夹角为( )A、 B、 C、 D、07. 设函数 的最小正周期为 ,则下列说法正确的是( )A、函数 的图像关于直线 对称 B、函数 的图像关于点 对称 C、函数 在 上单调递减 D、将函数 的图像向右平移 个单位,得到的新函数是偶函数8. 已知向量 夹角为 , , ,则 为( )A、1 B、 C、 D、39. 若 ,其中 ,则 的值为( )A、 B、 C、 D、10. 已知函数 , ,则函数 , 的值域为( )A、 B、 C、 D、11. 已知函数 的定义域为 ,当 时, ;当 时, ;当 时, ,则 的值为( )A、 B、 C、 D、12. 已知函数 , 有三个不同的零点 ,且 ,则 的值为( )A、 B、 C、 D、不能确定二、填空题
-
13. 的值为 .14. 在 中,若 , , ,则 .15. 已知函数 , 的图像的一个对称中心为 ,则 的值为 .16. 设函数 ,若存在互不相等的3个实数 ,使得 ,则实数 的取值范围为 .
三、解答题
-
17. 已知函数 ,它的部分图像如图所示.
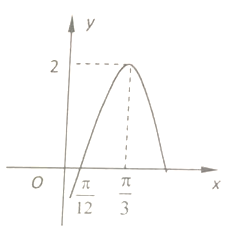 (1)、求函数 的解析式;(2)、将函数 图像上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图像向左平移 个单位,得到函数 的图像,求函数 , 的单调递增区间.18. 在 中, 是线段 的中点,已知 , , .(1)、用向量 表示向量 ;(2)、求 ;(3)、求 .19. 已知函数 满足 , 且 .(1)、求函数 的解析式及定义域;(2)、当 时,判断函数 的单调性并给予证明.20. 如图,一个水轮的半径为4米,水轮圆心 距离水面2米,已知水轮每分钟逆时针转动4圈,如果当水轮上点 从水中浮现(图中点 )开始计算时间.
(1)、求函数 的解析式;(2)、将函数 图像上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图像向左平移 个单位,得到函数 的图像,求函数 , 的单调递增区间.18. 在 中, 是线段 的中点,已知 , , .(1)、用向量 表示向量 ;(2)、求 ;(3)、求 .19. 已知函数 满足 , 且 .(1)、求函数 的解析式及定义域;(2)、当 时,判断函数 的单调性并给予证明.20. 如图,一个水轮的半径为4米,水轮圆心 距离水面2米,已知水轮每分钟逆时针转动4圈,如果当水轮上点 从水中浮现(图中点 )开始计算时间.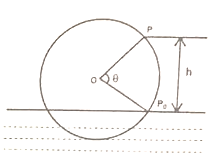 (1)、将点 距离水面的高度 (米)表示为时间 (秒)的函数;(2)、在水轮旋转一圈内,有多长时间点 离开水面?
(1)、将点 距离水面的高度 (米)表示为时间 (秒)的函数;(2)、在水轮旋转一圈内,有多长时间点 离开水面?